W tym zadaniu należy wyznaczyć wartość wyrażenia sin α–cos α, na podstawie iloczynu poszczególnych funkcji trygonometrycznych i przedziału wartości kąta α.
sin2α + cos2α = 1
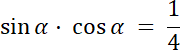
sin2α + cos2α = 1
![]()
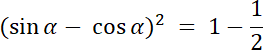
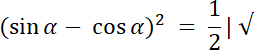
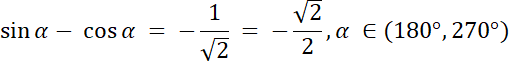

W tym zadaniu zapisz wyrażenie jako (sin α–cos α)2 = sin2α + cos2α–2 ⋅ sin α ⋅ cos α. Przy rozwiązywaniu, skorzystaj z twierdzenia jedynki trygonometrycznej: sin2α + cos2α = 1, a przy pierwiastkowaniu równania zwróć uwagę, że α ⋲ (180°, 270°) więc sin α < 0 i cos α < 0, więc
sin α–cos α < 0.

Ćwiczenie 3.
164Ćwiczenie 4.
164Ćwiczenie 5.
164Ćwiczenie 7.
165Ćwiczenie 9.
166Zadanie 1.
167Zadanie 2.
167Zadanie 3.
167Ćwiczenie 2.
171Zadanie 1.
173Zadanie 2.
174Zadanie 3.
173Zadanie 4.
173Zadanie 5.
173Zadanie 6.
173Zadanie 7.
173Zadanie 8.
173Zadanie 1.
179Zadanie 2.
179Zadanie 3.
180Zadanie 4.
180Zadanie 9.
180Ćwiczenie 4.
185Zadanie 1.
185Zadanie 2.
185Zadanie 3.
185Zadanie 4.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 11.
187Zadanie 18.
187Zadanie 20.
187
