Udowodnij, że równość
jest spełniona, jeśli w trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC.
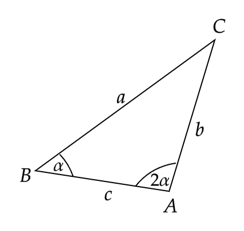
Trójkąt ABC jest równoramienny.
Trójkąt ABC jest wtedy szczególny, ponieważ miary jego kątów wynoszą
.
To kończy dowód.
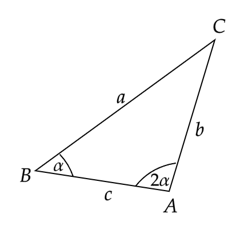
Wykonaj rysunek pomocniczy:
Zapis tezę zawartą w treści zadania za pomocą oznaczeń na rysunku.
Skorzystaj z twierdzenia sinusów w tym trójkącie.
Użyj wzoru na sinus podwojonego kąta i z powstałego równania oblicz wartość cosinusa.
Pomnóż na skos.
Skorzystaj z twierdzenia cosinusów w trójkącie ABC. Podstaw obliczoną wartość cosinusa.
Pomnóż całe równanie przez wartość mianownika i przenieś wszystkie wartości na lewą stronę równania.
Wyłącz wspólne czynniki przed nawias. Zauważ wzór skróconego mnożenia na różnicę kwadratów.
Zauważ, że aby równanie było równe zero, to przynajmniej jeden z nawiasów musi się zerować.
Oblicz pierwszy z nawiasów. Sprawdź czy spełnia on tezę zawartą w treści zadania.
Zauważ, że w takim przypadku trójkąt ABC jest równoramienny.
Oblicz miary kątów tego trójkąta.
Oznacza to, że trójkąt ABC jest szczególny, ponieważ miary jego kątów wynoszą
. Podstawa trójkąta jest o
razy dłuższa od długości jego ramienia.
Podstaw zapisane długości boków pod tezę i sprawdź czy lewa strona jest równa prawej.
Oblicz drugi z nawiasów. Sprawdź czy spełnia on tezę zawartą w treści zadania.
To kończy dowód.