Udowodnij, że sześciokąt ABCDEF o wierzchołkach
![]() ma środek symetrii
ma środek symetrii
Sześciokąt ma środek symetrii, gdy środki jego przeciwległych wierzchołków mają takie same współrzędne.
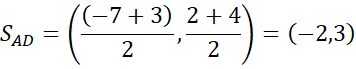
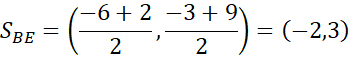
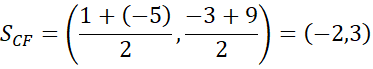
Wszystkie pary przeciwległych boków mają taki sam środek, więc sześciokąt jest symetryczny względem niego.
To kończy dowód.


Zadanie 1.5.
43Zadanie 1.6.
44Zadanie 1.7.
44Zadanie 1.8.
44Zadanie 1.9.
44Zadanie 1.10.
44Zadanie 1.11.
44Zadanie 1.12.
44Zadanie 1.13.
44Zadanie 1.14.
45Zadanie 1.18.
45Zadanie 1.19.
45Zadanie 1.20.
45Zadanie 1.21.
45Zadanie 2.1.
55Zadanie 2.2.
55Zadanie 2.3.
55Zadanie 2.4.
55Zadanie 2.5.
55Zadanie 2.6.
55Zadanie 2.7.
55Zadanie 2.8.
56Zadanie 2.9.
56Zadanie 2.10.
56Zadanie 2.14.
56Zadanie 2.15.
56Zadanie 2.17.
56Zadanie 3.1.
67Zadanie 3.2.
68Zadanie 3.3.
68Zadanie 3.4.
68Zadanie 3.5.
68Zadanie 3.7.
68Zadanie 3.12.
69Zadanie 3.14.
69Zadanie 3.16.
69Zadanie 3.17.
69Zadanie 4.1.
76Zadanie 4.2.
76Zadanie 4.3.
76Zadanie 4.4.
76Zadanie 4.6.
77Zadanie 4.9.
77Zadanie 4.14.
77Zadanie 4.16.
77Zadanie 4.17.
78Zadanie 5.2.
84Zadanie 5.3.
84Zadanie 5.8.
85Zadanie 5.14.
85Zadanie 5.19.
86Zadanie 6.3.
92Zadanie 6.4.
92Zadanie 6.7.
92Zadanie 6.9.
92Zadanie 6.11.
93Zadanie 6.14.
93Zadanie 6.15.
93Zadanie 6.16.
93Zadanie 7.1.
100Zadanie 7.2.
100Zadanie 7.3.
100Zadanie 7.5.
100Zadanie 7.6.
101Zadanie 7.8.
101Zadanie 7.10.
102Zadanie 7.11.
102Zadanie 7.12.
102Zadanie 7.15.
102Zadanie 8.2.
111Zadanie 8.3.
111Zadanie 8.10.
112Zadanie 8.14.
112Zadanie 33.
117Zadanie 34.
117Zadanie 35.
118Zadanie 36.
118Zadanie 37.
118Zadanie 47.
119Zadanie 64.
120
