Ustal, dla jakich wartości
![]() prosta o równaniu
prosta o równaniu
![]() przechodzi przez II, III i IV ćwiartkę układu współrzędnych?
przechodzi przez II, III i IV ćwiartkę układu współrzędnych?
![]()
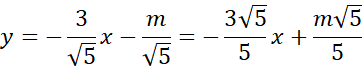
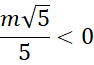
![]()

Podane równanie przedstaw w postaci kierunkowej:
![]() . Następnie zauważ, że aby prosta nie miała punktów wspólnych z I ćwiartką układu współrzędnych, to jej wykres musi być malejący, czyli współczynnik kierunkowy
. Następnie zauważ, że aby prosta nie miała punktów wspólnych z I ćwiartką układu współrzędnych, to jej wykres musi być malejący, czyli współczynnik kierunkowy
![]() ujemny, a wyraz wolny przecinać oś OY w ujemnym punkcie, czyli być ujemny. Na tej podstawie wyznacz wartość parametru
ujemny, a wyraz wolny przecinać oś OY w ujemnym punkcie, czyli być ujemny. Na tej podstawie wyznacz wartość parametru
![]() spełniającego oba warunki.
spełniającego oba warunki.

Zadanie 1.5.
43Zadanie 1.6.
44Zadanie 1.7.
44Zadanie 1.8.
44Zadanie 1.9.
44Zadanie 1.10.
44Zadanie 1.11.
44Zadanie 1.12.
44Zadanie 1.13.
44Zadanie 1.14.
45Zadanie 1.18.
45Zadanie 1.19.
45Zadanie 1.20.
45Zadanie 1.21.
45Zadanie 2.1.
55Zadanie 2.2.
55Zadanie 2.3.
55Zadanie 2.4.
55Zadanie 2.5.
55Zadanie 2.6.
55Zadanie 2.7.
55Zadanie 2.8.
56Zadanie 2.9.
56Zadanie 2.10.
56Zadanie 2.14.
56Zadanie 2.15.
56Zadanie 2.17.
56Zadanie 3.1.
67Zadanie 3.2.
68Zadanie 3.3.
68Zadanie 3.4.
68Zadanie 3.5.
68Zadanie 3.7.
68Zadanie 3.12.
69Zadanie 3.14.
69Zadanie 3.16.
69Zadanie 3.17.
69Zadanie 4.1.
76Zadanie 4.2.
76Zadanie 4.3.
76Zadanie 4.4.
76Zadanie 4.6.
77Zadanie 4.9.
77Zadanie 4.14.
77Zadanie 4.16.
77Zadanie 4.17.
78Zadanie 5.2.
84Zadanie 5.3.
84Zadanie 5.8.
85Zadanie 5.14.
85Zadanie 5.19.
86Zadanie 6.3.
92Zadanie 6.4.
92Zadanie 6.7.
92Zadanie 6.9.
92Zadanie 6.11.
93Zadanie 6.14.
93Zadanie 6.15.
93Zadanie 6.16.
93Zadanie 7.1.
100Zadanie 7.2.
100Zadanie 7.3.
100Zadanie 7.5.
100Zadanie 7.6.
101Zadanie 7.8.
101Zadanie 7.10.
102Zadanie 7.11.
102Zadanie 7.12.
102Zadanie 7.15.
102Zadanie 8.2.
111Zadanie 8.3.
111Zadanie 8.10.
112Zadanie 8.14.
112Zadanie 33.
117Zadanie 34.
117Zadanie 35.
118Zadanie 36.
118Zadanie 37.
118Zadanie 47.
119Zadanie 64.
120
