Zapisz równanie okręgu stycznego do osi
![]() , którego środek jest punktem przecięcia prostych
, którego środek jest punktem przecięcia prostych
![]() i
i
![]() .
.
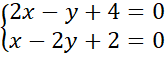
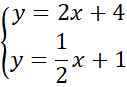
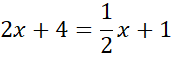
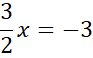
![]()
![]()
![]()
![]()
![]()

Zauważ, że skoro okrąg jest styczny do osi
![]() , to pierwsza współrzędna środka jest równa długości jego promienia. Wyznacz punkt przecięcia podanych prostych rozwiązując powstały układ równań.
, to pierwsza współrzędna środka jest równa długości jego promienia. Wyznacz punkt przecięcia podanych prostych rozwiązując powstały układ równań.
Następnie skorzystaj z tego, że równanie okręgu można opisać za pomocą wzoru:
![]() , gdzie
, gdzie
![]() to środek okręgu, a
to środek okręgu, a
![]() to jego promień.
to jego promień.

Zadanie 1.5.
43Zadanie 1.6.
44Zadanie 1.7.
44Zadanie 1.8.
44Zadanie 1.9.
44Zadanie 1.10.
44Zadanie 1.11.
44Zadanie 1.12.
44Zadanie 1.13.
44Zadanie 1.14.
45Zadanie 1.18.
45Zadanie 1.19.
45Zadanie 1.20.
45Zadanie 1.21.
45Zadanie 2.1.
55Zadanie 2.2.
55Zadanie 2.3.
55Zadanie 2.4.
55Zadanie 2.5.
55Zadanie 2.6.
55Zadanie 2.7.
55Zadanie 2.8.
56Zadanie 2.9.
56Zadanie 2.10.
56Zadanie 2.14.
56Zadanie 2.15.
56Zadanie 2.17.
56Zadanie 3.1.
67Zadanie 3.2.
68Zadanie 3.3.
68Zadanie 3.4.
68Zadanie 3.5.
68Zadanie 3.7.
68Zadanie 3.12.
69Zadanie 3.14.
69Zadanie 3.16.
69Zadanie 3.17.
69Zadanie 4.1.
76Zadanie 4.2.
76Zadanie 4.3.
76Zadanie 4.4.
76Zadanie 4.6.
77Zadanie 4.9.
77Zadanie 4.14.
77Zadanie 4.16.
77Zadanie 4.17.
78Zadanie 5.2.
84Zadanie 5.3.
84Zadanie 5.8.
85Zadanie 5.14.
85Zadanie 5.19.
86Zadanie 6.3.
92Zadanie 6.4.
92Zadanie 6.7.
92Zadanie 6.9.
92Zadanie 6.11.
93Zadanie 6.14.
93Zadanie 6.15.
93Zadanie 6.16.
93Zadanie 7.1.
100Zadanie 7.2.
100Zadanie 7.3.
100Zadanie 7.5.
100Zadanie 7.6.
101Zadanie 7.8.
101Zadanie 7.10.
102Zadanie 7.11.
102Zadanie 7.12.
102Zadanie 7.15.
102Zadanie 8.2.
111Zadanie 8.3.
111Zadanie 8.10.
112Zadanie 8.14.
112Zadanie 33.
117Zadanie 34.
117Zadanie 35.
118Zadanie 36.
118Zadanie 37.
118Zadanie 47.
119Zadanie 64.
120
