Oblicz współrzędne dwóch sąsiednich wierzchołków, jeśli wszystkie wierzchołki ośmiokąta foremnego leżą na okręgu o środku w punkcie (0,0). Jednym z wierzchołków ośmiokąta jest punkt (4,0).
![]()
![]()
Prosta przechodząca przez środki boków AC i EG:
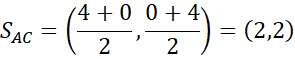
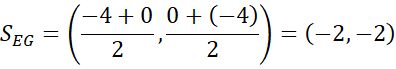
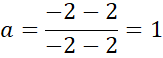
![]()
![]()
![]()
Punkt B:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Skorzystaj ze wzoru na długość odcinka, aby wyznaczyć promień podanego okręgu, a następnie zauważ, że punkty A, C, E, G będą leżeć na osiach układu współrzędnych o będą odległe o 4 jednostki od początku układu współrzędnych. Następnie wyznacz równanie prostej przechodzącej przez środku odcinków AC i EG oraz jednocześnie przez punkty B i F. Następnie pod długość odcinka SB podstaw znane wartości i z powstałego równania wyznacz współrzędne punktów B i F oraz analogicznie punktów D i H.

Zadanie 1.5.
43Zadanie 1.6.
44Zadanie 1.7.
44Zadanie 1.8.
44Zadanie 1.9.
44Zadanie 1.10.
44Zadanie 1.11.
44Zadanie 1.12.
44Zadanie 1.13.
44Zadanie 1.14.
45Zadanie 1.18.
45Zadanie 1.19.
45Zadanie 1.20.
45Zadanie 1.21.
45Zadanie 2.1.
55Zadanie 2.2.
55Zadanie 2.3.
55Zadanie 2.4.
55Zadanie 2.5.
55Zadanie 2.6.
55Zadanie 2.7.
55Zadanie 2.8.
56Zadanie 2.9.
56Zadanie 2.10.
56Zadanie 2.14.
56Zadanie 2.15.
56Zadanie 2.17.
56Zadanie 3.1.
67Zadanie 3.2.
68Zadanie 3.3.
68Zadanie 3.4.
68Zadanie 3.5.
68Zadanie 3.7.
68Zadanie 3.12.
69Zadanie 3.14.
69Zadanie 3.16.
69Zadanie 3.17.
69Zadanie 4.1.
76Zadanie 4.2.
76Zadanie 4.3.
76Zadanie 4.4.
76Zadanie 4.6.
77Zadanie 4.9.
77Zadanie 4.14.
77Zadanie 4.16.
77Zadanie 4.17.
78Zadanie 5.2.
84Zadanie 5.3.
84Zadanie 5.8.
85Zadanie 5.14.
85Zadanie 5.19.
86Zadanie 6.3.
92Zadanie 6.4.
92Zadanie 6.7.
92Zadanie 6.9.
92Zadanie 6.11.
93Zadanie 6.14.
93Zadanie 6.15.
93Zadanie 6.16.
93Zadanie 7.1.
100Zadanie 7.2.
100Zadanie 7.3.
100Zadanie 7.5.
100Zadanie 7.6.
101Zadanie 7.8.
101Zadanie 7.10.
102Zadanie 7.11.
102Zadanie 7.12.
102Zadanie 7.15.
102Zadanie 8.2.
111Zadanie 8.3.
111Zadanie 8.10.
112Zadanie 8.14.
112Zadanie 33.
117Zadanie 34.
117Zadanie 35.
118Zadanie 36.
118Zadanie 37.
118Zadanie 47.
119Zadanie 64.
120
