Wykaż, że trójkąt o wierzchołkach
![]() jest równoboczny. Napisz równanie okręgu symetrycznego względem początku układu współrzędnych do okręgu opisanego na tym trójkącie.
jest równoboczny. Napisz równanie okręgu symetrycznego względem początku układu współrzędnych do okręgu opisanego na tym trójkącie.

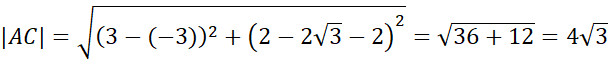
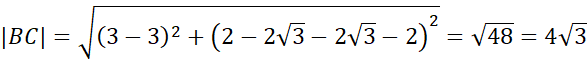
![]() - trójkąt ma wszystkie boki równe, więc jest równoboczny.
- trójkąt ma wszystkie boki równe, więc jest równoboczny.
To kończy dowód.
![]()
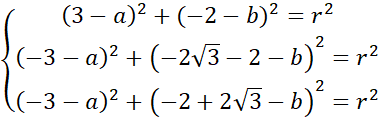
![]()
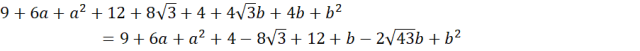
![]()
![]()
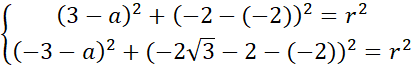
![]()
![]()
![]()
![]()

Skorzystaj ze wzoru na długość odcinka:
![]() i na tej podstawie oblicz długości boków AB, AC i BC oraz tego, że po odbiciu punktu względem początku układu współrzędnych każda z jego współrzędnych zmieni znak na przeciwny.
i na tej podstawie oblicz długości boków AB, AC i BC oraz tego, że po odbiciu punktu względem początku układu współrzędnych każda z jego współrzędnych zmieni znak na przeciwny.
Następnie skorzystaj z tego, że równanie okręgu można opisać za pomocą wzoru:
![]() , gdzie
, gdzie
![]() to środek okręgu, a
to środek okręgu, a
![]() to jego promień. Podane punkty podstaw pod ten wzór. Zauważ, że powstanie układ trzech równań z trzema niewiadomymi, rozwiąż go i zapisz szukane równanie okręgu.
to jego promień. Podane punkty podstaw pod ten wzór. Zauważ, że powstanie układ trzech równań z trzema niewiadomymi, rozwiąż go i zapisz szukane równanie okręgu.

Zadanie 1.5.
43Zadanie 1.6.
44Zadanie 1.7.
44Zadanie 1.8.
44Zadanie 1.9.
44Zadanie 1.10.
44Zadanie 1.11.
44Zadanie 1.12.
44Zadanie 1.13.
44Zadanie 1.14.
45Zadanie 1.18.
45Zadanie 1.19.
45Zadanie 1.20.
45Zadanie 1.21.
45Zadanie 2.1.
55Zadanie 2.2.
55Zadanie 2.3.
55Zadanie 2.4.
55Zadanie 2.5.
55Zadanie 2.6.
55Zadanie 2.7.
55Zadanie 2.8.
56Zadanie 2.9.
56Zadanie 2.10.
56Zadanie 2.14.
56Zadanie 2.15.
56Zadanie 2.17.
56Zadanie 3.1.
67Zadanie 3.2.
68Zadanie 3.3.
68Zadanie 3.4.
68Zadanie 3.5.
68Zadanie 3.7.
68Zadanie 3.12.
69Zadanie 3.14.
69Zadanie 3.16.
69Zadanie 3.17.
69Zadanie 4.1.
76Zadanie 4.2.
76Zadanie 4.3.
76Zadanie 4.4.
76Zadanie 4.6.
77Zadanie 4.9.
77Zadanie 4.14.
77Zadanie 4.16.
77Zadanie 4.17.
78Zadanie 5.2.
84Zadanie 5.3.
84Zadanie 5.8.
85Zadanie 5.14.
85Zadanie 5.19.
86Zadanie 6.3.
92Zadanie 6.4.
92Zadanie 6.7.
92Zadanie 6.9.
92Zadanie 6.11.
93Zadanie 6.14.
93Zadanie 6.15.
93Zadanie 6.16.
93Zadanie 7.1.
100Zadanie 7.2.
100Zadanie 7.3.
100Zadanie 7.5.
100Zadanie 7.6.
101Zadanie 7.8.
101Zadanie 7.10.
102Zadanie 7.11.
102Zadanie 7.12.
102Zadanie 7.15.
102Zadanie 8.2.
111Zadanie 8.3.
111Zadanie 8.10.
112Zadanie 8.14.
112Zadanie 33.
117Zadanie 34.
117Zadanie 35.
118Zadanie 36.
118Zadanie 37.
118Zadanie 47.
119Zadanie 64.
120
