W tym ćwiczeniu musisz udowodnić podaną nierówność.
Musisz udowodnić następującą nierówność:
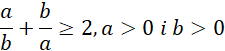
Skoro a i b są dodatnie, możesz wymnożyć nierówność przez ich iloczyn, bez straty ogólności otrzymując:
![]()
![]()
![]()
Co kończy dowód.

Ostatnia linijka dowodu wynika z tego, że kwadrat dowolnej liczby rzeczywistej jest liczbą nieujemną.

Ćwiczenie 1.
7Ćwiczenie 2.
7Ćwiczenie 3.
9Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Zadanie 6.
11Zadanie 7.
10Zadanie 8.
11Ćwiczenie 1.
12Ćwiczenie 2.
15Zadanie 1.
16Zadanie 2.
16Zadanie 3.
16Zadanie 4.
16Zadanie 5.
16Zadanie 1.
20Zadanie 2.
20Zadanie 3.
20Zadanie 4.
20Zadanie 5.
20Zadanie 6.
20Ćwiczenie 2.
21Zadanie 1.
24Zadanie 2.
24Zadanie 3.
24Zadanie 4.
25Ćwiczenie 1.
26Zadanie 1.
30Zadanie 2.
30Zadanie 3.
30Zadanie 4.
31Zadanie 5.
31Zadanie 9.
31Zadanie 10.
31Ćwiczenie 1.
38Ćwiczenie 2.
40Zadanie 1.
41Zadanie 2.
42Zadanie 3.
42Zadanie 4.
42Zadanie 5.
42Zadanie 6.
42Ćwiczenie 3.
53Ćwiczenie 5.
54Zadanie 1.
55Zadanie 2.
55Zadanie 3.
55Zadanie 4.
55Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 8.
56Zadanie 9.
56Zadanie 1.
62Zadanie 2.
62Zadanie 3.
62Zadanie 4.
62Zadanie 5.
63Zadanie 6.
63Zadanie 7.
63Zadanie 8.
63Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 7.
68Zadanie 8.
68Zadanie 9.
68Zadanie 10.
68Zadanie 11.
68Zadanie 12.
68Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Zadanie 18.
72Zadanie 19.
72Zadanie 24.
72
