W tym zadaniu musisz udowodnić prawdziwość implikacji.
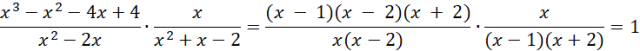

Ponieważ rozważasz
![]()
Nie masz sytuacji, w której dzielisz przez zero, możesz zatem wykonać odpowiednio obliczenia, które doprowadzą do wykazania podanej implikacji. Przy rozkładaniu wielomianu
![]()
Na czynniki zauważ, że jedynka jest miejscem zerowym tego wielomianu, a następnie porównaj współczynniki przy potęgach, aby rozłożyć całość:
![]()
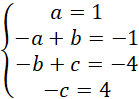
![]()
Ostatecznie:
![]()
Gdzie druga równość wynika ze wzoru skróconego mnożenia:
![]()

Ćwiczenie 1.
7Ćwiczenie 2.
7Ćwiczenie 3.
9Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Zadanie 6.
11Zadanie 7.
10Zadanie 8.
11Ćwiczenie 1.
12Ćwiczenie 2.
15Zadanie 1.
16Zadanie 2.
16Zadanie 3.
16Zadanie 4.
16Zadanie 5.
16Zadanie 1.
20Zadanie 2.
20Zadanie 3.
20Zadanie 4.
20Zadanie 5.
20Zadanie 6.
20Ćwiczenie 2.
21Zadanie 1.
24Zadanie 2.
24Zadanie 3.
24Zadanie 4.
25Ćwiczenie 1.
26Zadanie 1.
30Zadanie 2.
30Zadanie 3.
30Zadanie 4.
31Zadanie 5.
31Zadanie 9.
31Zadanie 10.
31Ćwiczenie 1.
38Ćwiczenie 2.
40Zadanie 1.
41Zadanie 2.
42Zadanie 3.
42Zadanie 4.
42Zadanie 5.
42Zadanie 6.
42Ćwiczenie 3.
53Ćwiczenie 5.
54Zadanie 1.
55Zadanie 2.
55Zadanie 3.
55Zadanie 4.
55Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 8.
56Zadanie 9.
56Zadanie 1.
62Zadanie 2.
62Zadanie 3.
62Zadanie 4.
62Zadanie 5.
63Zadanie 6.
63Zadanie 7.
63Zadanie 8.
63Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 7.
68Zadanie 8.
68Zadanie 9.
68Zadanie 10.
68Zadanie 11.
68Zadanie 12.
68Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Zadanie 18.
72Zadanie 19.
72Zadanie 24.
72
