W tym ćwiczeniu musisz wykazać, że istnieje tylko jeden parametr spełniający daną tożsamość.
![]()

Z informacji o dziedzinie funkcji
![]() wnioskujesz, że dla
wnioskujesz, że dla
![]() mianownika wynosi zero:
mianownika wynosi zero:
![]()
![]()
![]()
![]()
Sprawdzasz:
![]()
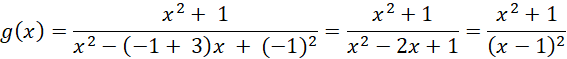
Gdzie dziedziną jest zbiór
![]() .
.
Sprawdzasz:
![]()
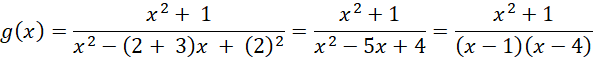
Gdzie dziedziną jest zbiór
![]() . Zatem widzisz, że z powyższych rozważań istnieje dokładnie jeden taki parametr
. Zatem widzisz, że z powyższych rozważań istnieje dokładnie jeden taki parametr
![]() spełniający zadany warunek.
spełniający zadany warunek.

Ćwiczenie 1.
7Ćwiczenie 2.
7Ćwiczenie 3.
9Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Zadanie 6.
11Zadanie 7.
10Zadanie 8.
11Ćwiczenie 1.
12Ćwiczenie 2.
15Zadanie 1.
16Zadanie 2.
16Zadanie 3.
16Zadanie 4.
16Zadanie 5.
16Zadanie 1.
20Zadanie 2.
20Zadanie 3.
20Zadanie 4.
20Zadanie 5.
20Zadanie 6.
20Ćwiczenie 2.
21Zadanie 1.
24Zadanie 2.
24Zadanie 3.
24Zadanie 4.
25Ćwiczenie 1.
26Zadanie 1.
30Zadanie 2.
30Zadanie 3.
30Zadanie 4.
31Zadanie 5.
31Zadanie 9.
31Zadanie 10.
31Ćwiczenie 1.
38Ćwiczenie 2.
40Zadanie 1.
41Zadanie 2.
42Zadanie 3.
42Zadanie 4.
42Zadanie 5.
42Zadanie 6.
42Ćwiczenie 3.
53Ćwiczenie 5.
54Zadanie 1.
55Zadanie 2.
55Zadanie 3.
55Zadanie 4.
55Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 8.
56Zadanie 9.
56Zadanie 1.
62Zadanie 2.
62Zadanie 3.
62Zadanie 4.
62Zadanie 5.
63Zadanie 6.
63Zadanie 7.
63Zadanie 8.
63Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 7.
68Zadanie 8.
68Zadanie 9.
68Zadanie 10.
68Zadanie 11.
68Zadanie 12.
68Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Zadanie 18.
72Zadanie 19.
72Zadanie 24.
72
