W tym zadaniu należy wyznaczyć wartość parametru na podstawie wykresu funkcji.
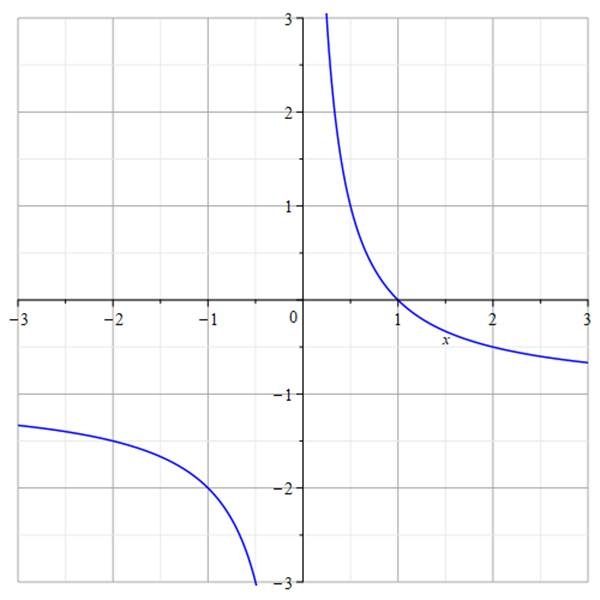
Wykres funkcji:
![]()
![]()

Dziedziną funkcji są
![]() . Najpierw musisz narysować wykres funkcji
. Najpierw musisz narysować wykres funkcji
![]() . Zacznij od uproszczenia wzoru funkcji:
. Zacznij od uproszczenia wzoru funkcji:
![]()
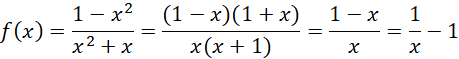
Z tej postaci widać, że funkcja elementarna
![]() została przesunięta o wektor [0,-1]. Branie wartości bezwzględnej oznacza, że część wykresu znajdującą się pod osią OX musisz „odbić” ponad tę oś. Z narysowanego wykresu odczytasz, że równanie ma dwa rozwiązania różnych znaków wtedy i tylko wtedy, gdy:
została przesunięta o wektor [0,-1]. Branie wartości bezwzględnej oznacza, że część wykresu znajdującą się pod osią OX musisz „odbić” ponad tę oś. Z narysowanego wykresu odczytasz, że równanie ma dwa rozwiązania różnych znaków wtedy i tylko wtedy, gdy:
![]()
![]()
![]()
![]()
![]()
![]()

Ćwiczenie 1.
7Ćwiczenie 2.
7Ćwiczenie 3.
9Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Zadanie 6.
11Zadanie 7.
10Zadanie 8.
11Ćwiczenie 1.
12Ćwiczenie 2.
15Zadanie 1.
16Zadanie 2.
16Zadanie 3.
16Zadanie 4.
16Zadanie 5.
16Zadanie 1.
20Zadanie 2.
20Zadanie 3.
20Zadanie 4.
20Zadanie 5.
20Zadanie 6.
20Ćwiczenie 2.
21Zadanie 1.
24Zadanie 2.
24Zadanie 3.
24Zadanie 4.
25Ćwiczenie 1.
26Zadanie 1.
30Zadanie 2.
30Zadanie 3.
30Zadanie 4.
31Zadanie 5.
31Zadanie 9.
31Zadanie 10.
31Ćwiczenie 1.
38Ćwiczenie 2.
40Zadanie 1.
41Zadanie 2.
42Zadanie 3.
42Zadanie 4.
42Zadanie 5.
42Zadanie 6.
42Ćwiczenie 3.
53Ćwiczenie 5.
54Zadanie 1.
55Zadanie 2.
55Zadanie 3.
55Zadanie 4.
55Zadanie 5.
56Zadanie 6.
56Zadanie 7.
56Zadanie 8.
56Zadanie 9.
56Zadanie 1.
62Zadanie 2.
62Zadanie 3.
62Zadanie 4.
62Zadanie 5.
63Zadanie 6.
63Zadanie 7.
63Zadanie 8.
63Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 7.
68Zadanie 8.
68Zadanie 9.
68Zadanie 10.
68Zadanie 11.
68Zadanie 12.
68Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Zadanie 18.
72Zadanie 19.
72Zadanie 24.
72
