Znajdź największy wspólny dzielnik, skróć ułamki do ułamków nieskracalnych.
NWD kolejnych ułamków: 5, 16, 18, 12, 42, 27.

Poszukaj liczby, przez którą można podzielić i licznik, i mianownik:
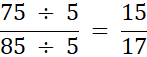
Otrzymaliśmy ułamek nieskracalny. Mimo że 15 można podzielić jeszcze przez 5, z 17 nic nie możemy już zrobić. Największym wspólnym dzielnikiem jest 5. Następnie przykłady wykonaj analogicznie:
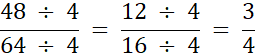
Największym wspólnym dzielnikiem jest iloraz 4 • 4 = 16
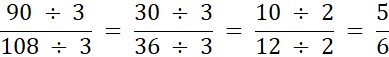
Największym wspólnym dzielnikiem jest iloraz 3 • 3 • 2 = 18
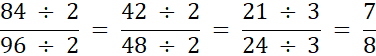
Największym wspólnym dzielnikiem jest iloraz 2 • 2 • 3 = 12
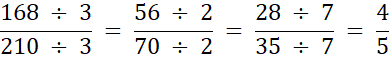
Największym wspólnym dzielnikiem jest iloraz 7 • 2 • 3 = 42
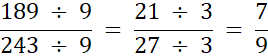
Największym wspólnym dzielnikiem jest iloraz 9 • 3 = 27
Często do stwierdzenia, przez co można podzielić ułamek, przydają się cechy podzielności liczb:
- Liczba jest podzielna przez 5, gdy jej cyfrą jedności jest 0 lub 5.
- Liczba jest podzielna przez 2, gdy jej cyfrą jedności jest 0, 2, 4, 6 lub 8.
- Jeśli suma cyfr danej liczby dzieli się przez 3, to ta liczba też się dzieli przez 3. Jeżeli suma cyfr danej liczby dzieli się przez 9, to ta liczba też dzieli się przez 9.

Ćwiczenie 1
68Ćwiczenie 2
69Ćwiczenie 3
70Ćwiczenie 4
70Ćwiczenie 5
71Zadanie 1
73Zadanie 2
72Zadanie 3
72Zadanie 4
72Zadanie 5
72Ćwiczenie 1
74Ćwiczenie 2
74Ćwiczenie 3
74Zadanie 1
75Zadanie 8
75Zadanie 9
75Ćwiczenie 1
77Zadanie 1
79Zadanie 3
79Zadanie 6
79Ćwiczenie 2
81Ćwiczenie 4
82Ćwiczenie 5
82Ćwiczenie 1
85Ćwiczenie 2
86Zadanie 1
87Zadanie 2
87Zadanie 3
87Zadanie 6
87Ćwiczenie 1
88Ćwiczenie 2
88Zadanie 1
89Ćwiczenie 1
90Ćwiczenie 2
91Ćwiczenie 3
91Ćwiczenie 4
91Ćwiczenie 5
92Zadanie 3
93Zadanie 5
93Zadanie 6
93Zadanie 7
93Ćwiczenie 1
95Zadanie 4
96Zadanie 5
96Ćwiczenie 1
98Zadanie 5
99Zadanie 7
99Zadanie 8
99Ćwiczenie 1
101Ćwiczenie 2
101Ćwiczenie 3
102Ćwiczenie 4
102Zadanie 7
103Ćwiczenie 1
104Ćwiczenie 2
105Ćwiczenie 3
105Zadanie 4
105Zadanie 6
106Zadanie 7
106Zadanie 10
106Ćwiczenie 109
109Zadanie 7
109Zadanie 6
112Zadanie 12
112
