W tym zadaniu musisz obliczyć objętość i pole powierzchni ostrosłupa prawidłowego trójkątnego, wiedząc, że jego krawędź boczna ma długość 13 oraz wysokość 6.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
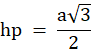
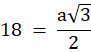
![]()
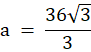
![]()
![]()
![]()
![]()
![]()
![]()
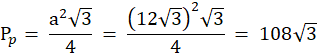
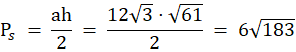
![]()
![]()
![]()
![]()
![]()

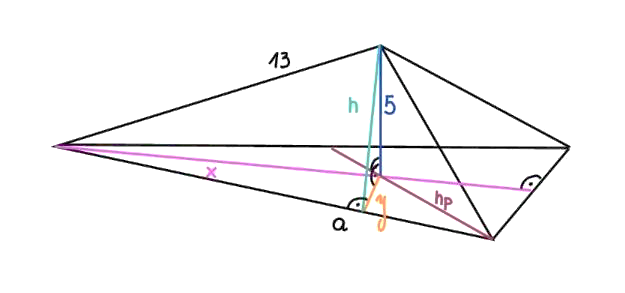
Zauważ, że podstawą ostrosłupa prawidłowego trójkątnego jest trójkąt równoboczny.
Wyznacz długość x, stosując twierdzenie Pitagorasa.
Wiedząc, że odcinek oznaczony jako x stanowi ![]()
Ze wzoru na długość wysokości trójkąta równobocznego oblicz długość a.
Wiedząc, że odcinek „y” jest ![]()
Z twierdzenia Pitagorasa oblicz wysokość h.
Oblicz pole podstawy ostrosłupa, jednej ściany bocznej, a następnie pole całkowite bryły.
Oblicz objętość ostrosłupa korzystając ze wzoru.
Przyjmij oznaczenia jak na rysunku:

Zadanie 2
234Zadanie 3
234Zadanie 4
234Zadanie 5
234Zadanie 6
234Zadanie 7
235Zadanie 8
235Zadanie 9
235Zadanie 10
235Zadanie 13
235Zadanie 14
235Zadanie 15
236Zadanie 17
162Zadanie 18
236Zadanie 24
162Zadanie 25
237Zadanie 26
238Zadanie 27
238Zadanie 1
243Zadanie 3
243Zadanie 4
244Zadanie 5
244Zadanie 6
244Zadanie 7
244Zadanie 8
244Zadanie 9
244Zadanie 10
245Zadanie 12
245Zadanie 14
245Zadanie 15
245Zadanie 16
162Zadanie 2
249Zadanie 3
162Zadanie 4
250Zadanie 6
250Zadanie 14
251Zadanie 1
256Zadanie 2
256Zadanie 9
257Zadanie 11
257Zadanie 16
162Zadanie 1
261Zadanie 4
262Zadanie 5
262Zadanie 8
262Zadanie 11
263Zadanie 12
263
