W tym zadaniu podaj, ile wynoszą funkcje trygonometryczne kąta A w trójkącie ABC, który ma kąt prosty przy wierzchołku C i boki długości |BC| = 6 i |AB| = 7.
![]()
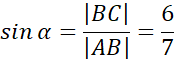
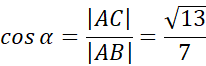
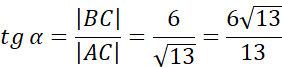

Aby rozwiązać to zadanie stwórz rysunek pomocniczy, wyznacz miarę brakującego boku z twierdzenia Pitagorasa i skorzystaj z definicji sinusa, cosinusa oraz tangensa kąta ostrego w trójkącie prostokątnym.
Sinusem kąta ostrego α nazywamy stosunek długości przyprostokątnej, która leży naprzeciwko tego kąta do długości przeciwprostokątnej. Oznaczamy jako sinα.
Cosinusem kąta ostrego α nazywamy stosunek długości przyprostokątnej, która przylega do tego kąta do długości przeciwprostokątnej. Oznaczamy jako cosα.
Tangensem kąta ostrego α nazywamy stosunek długości przyprostokątnej, która leży naprzeciwko tego kąta do długości przyprostokątnej przylegającej do niego. Oznaczamy jako tgα.

Zadanie 1.1.
229Zadanie 1.3.
229Zadanie 1.4.
229Zadanie 1.5.
229Zadanie 1.6.
229Zadanie 1.7.
230Zadanie 1.8.
230Zadanie 1.9.
230Zadanie 1.10.
230Zadanie 1.11.
230Zadanie 1.12.
231Zadanie 1.16.
231Zadanie 1.17.
231Zadanie 1.18.
231Zadanie 1.19.
231Zadanie 1.20.
231Zadanie 2.1.
237Zadanie 2.2.
237Zadanie 2.3.
237Zadanie 2.4.
237Zadanie 2.6.
238Zadanie 2.7.
238Zadanie 2.8.
238Zadanie 2.9.
238Zadanie 3.12.
244Zadanie 3.19.
245Zadanie 4.5.
251Zadanie 4.6.
251Zadanie 4.18.
253Zadanie 5.2.
262Zadanie 5.3.
262Zadanie 5.5.
262Zadanie 5.6.
263Zadanie 5.7.
263Zadanie 5.8.
263Zadanie 5.9.
263Zadanie 5.10.
263Zadanie 5.11.
263Zadanie 6.1.
268Zadanie 6.2.
268Zadanie 6.3.
269Zadanie 6.4.
269Zadanie 6.9.
269Zadanie 6.14.
269Zadanie 6.15.
270Zadanie 28.
274Zadanie 29.
274Zadanie 30.
274Zadanie 40.
275Zadanie 41.
275Zadanie 51.
276
