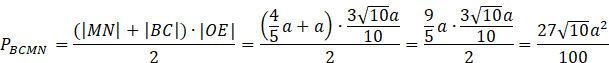
![]() – trapez równoramienny
– trapez równoramienny
![]()
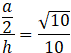
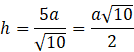
![]()
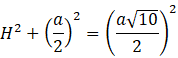
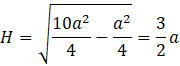
![]()
![]()
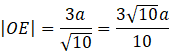
![]()
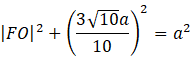
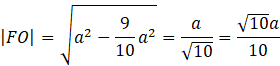
![]() z cechy kąt, kąt, kąt
z cechy kąt, kąt, kąt
![]()
![]()
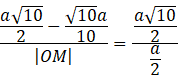
![]()
![]()
![]()
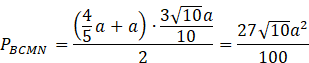
ODP: Płaszczyzna
![]() tworzy trapez równoramienny, którego pole jest równe
tworzy trapez równoramienny, którego pole jest równe
![]()

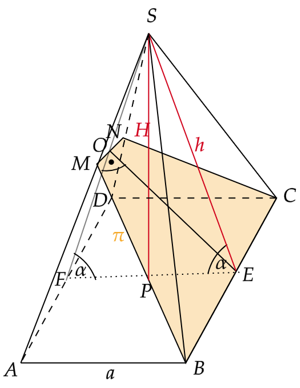
Wykonaj rysunek.
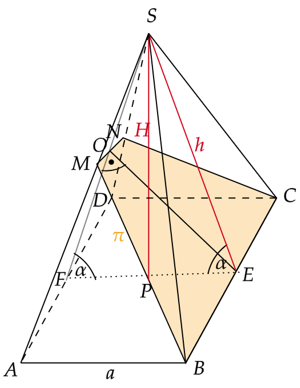
Zauważ, że płaszczyzna
![]() utworzyła figurę
utworzyła figurę
![]() będącą trapezem równoramiennym. Boki BC i MN są równoległe i są jego podstawami, a boki MB i NC są jego ramieniami i są równe, ponieważ są długościami wysokości takich samych ścian bocznych ostrosłupa.
będącą trapezem równoramiennym. Boki BC i MN są równoległe i są jego podstawami, a boki MB i NC są jego ramieniami i są równe, ponieważ są długościami wysokości takich samych ścian bocznych ostrosłupa.
Skorzystaj z własności funkcji trygonometrycznych w trójkącie PSE.
![]()
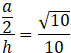
![]()
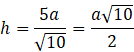
Skorzystaj z twierdzenia Pitagorasa w trójkącie PSE i oblicz długość boku PS, czyli wysokość ostrosłupa.
![]()
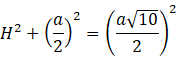
![]()
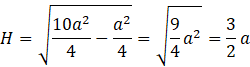
Zauważ, że pole trójkąta SFE możesz obliczyć na dwa sposoby.
![]()
![]()
![]()
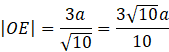
Skorzystaj z twierdzenia Pitagorasa w trójkącie FOE i oblicz długość boku FO.
![]()
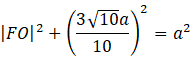
![]()
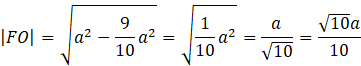
Zauważ, że trójkąty
![]() są podobne z cechy kąt, kąt, kąt
są podobne z cechy kąt, kąt, kąt
![]()
![]()
![]()
Oblicz długość boku OM.
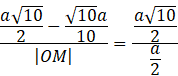
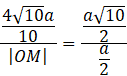
![]()
![]()
![]()
Oblicz długość boku MN.
![]()
Oblicz pole trapezu BCMN utworzonego przez płaszczyznę
![]() .
.