Matura z matematyki. Arkusz próbny. Poziom rozszerzony. 2022

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 11 - strona 20

Oblicz pole i obwód trapezu ABCD na którym opisano okrąg o promieniu 𝑅=5, w którym podstawy mają długość 𝐴𝐵 i 𝐶𝐷, gdzie |𝐴𝐵|>|𝐶𝐷|, ramię 𝐵𝐶 jest równe 6, a miary kątów 𝐵𝐴𝐶 i 𝐴𝐵𝐶 tego trapezu spełniają warunek $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

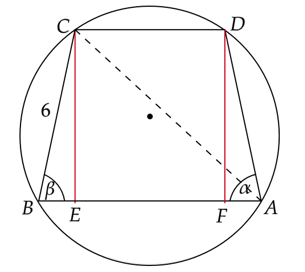
Trapez ABCD równoramienny.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

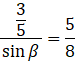
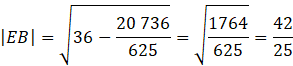
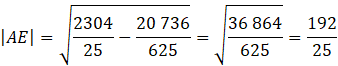
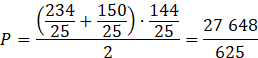
ODP: Pole trapezu ABCD wynosi $\text{[math]}$ , a obwód $\text{[math]}$ .

Wykonaj rysunek pomocniczy.

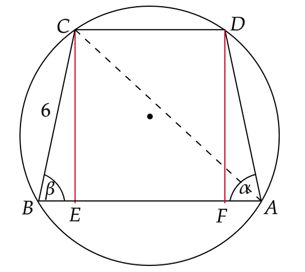
Skorzystaj z tego, że suma miar kątów w trójkącie wynosi $\text{[math]}$ i oblicz miarę kąta ACB.

$\text{[math]}$

Skorzystaj z tego, że na trapezie można opisać okrąg, więc suma miar przeciwległych kątów wynosi $\text{[math]}$ . Oblicz miarę kąta ADC.

$\text{[math]}$

Skorzystaj z tego, że suma miar kątów leżących przy jednym ramieniu trapezu wynosi $\text{[math]}$ . Oblicz miarę kąta ACD.

$\text{[math]}$

Oblicz miarę kąta BCD.

$\text{[math]}$

Zauważ, że $\text{[math]}$ , więc $\text{[math]}$ .

Oznacza to, że trapez ABCD równoramienny.

Skorzystaj z twierdzenia sinusów w trójkącie ABC i oblicz $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Skorzystaj z tego, że $\text{[math]}$ i oblicz $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

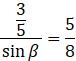
Skorzystaj z twierdzenia sinusów w trójkącie ABC i oblicz długość boku AC.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

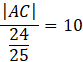
Skorzystaj z własności funkcji trygonometrycznych w trójkącie BCE i oblicz długość wysokości trapezu.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Skorzystaj z twierdzenia Pitagorasa w trójkącie BCE i oblicz długość boku BE.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

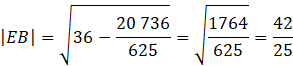
Skorzystaj z twierdzenia Pitagorasa w trójkącie ACE i oblicz długość boku AE.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

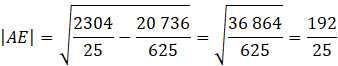
Oblicz długości podstaw trapezu ABCD.

$\text{[math]}$

$\text{[math]}$

Oblicz pole i obwód trapezu ABCD.

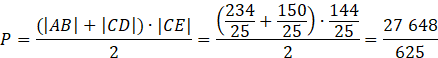
$\text{[math]}$

$\text{[math]}$

Zadanie 14, strona 194, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 13, strona 224, Matematyka z plusem. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 5.19., strona 41, Prosto do matury. Matematyka. Klasa 2. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 5, strona 36, Matematyka z Plusem. Klasa 4. Zeszyt ćwiczeń. Wersja B. Część 2/2 - rozwiązania i odpowiedzi

Zadanie 16., strona 146, Matematyka. Klasa 1. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 22., strona 228, Matematyka. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie S1, strona 159, Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 2., strona 51, Matematyka z plusem. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 5, strona 10, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Zadanie 9., strona 83, Matematyka wokół nas. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

4

Zadanie 2

5

5

5

7

8

9

10

12

14

16

18

20

22

Pełny spis treści