W tym zadaniu udowodnij, że czworokąt, którego wierzchołkami są te punkty, jest trapezem, wiedząc, że punkty A, B, C, D leżą na okręgu oraz |AB| = |CD|.
|∢ADB| = |∢CBD|
Proste zawierające boki BC oraz AD są równoległe, ponieważ kąty naprzemianległe ADB i CBD są równe. Boki BC oraz AD są równoległe. ABCD– jest zatem trapezem

Dla kątów opartych na tym samym łuku miara kąta środkowego jest zawsze 2 razy większa od miary kąta wpisanego. Tę zależność nazywamy twierdzeniem o kątach wpisanym i środkowym opartych na tym samym łuku.
Przyjmij oznaczenia widoczne na rysunku:
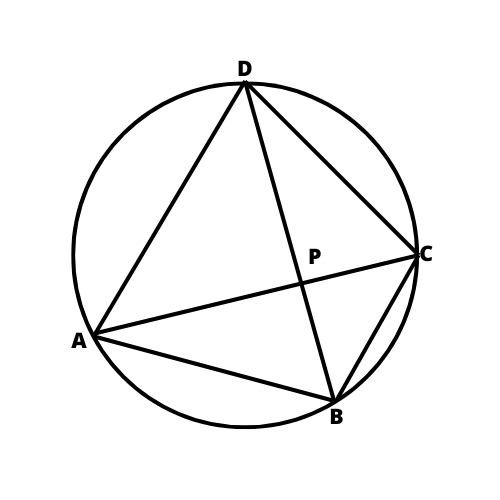
Kąty wpisane są równe, gdy oparte są na tych samych łukach o tej samej długości.
|∢ADB| = |∢CBD|
Proste zawierające boki BC oraz AD są równoległe, ponieważ kąty naprzemianległe ADB i CBD są równe. Boki BC oraz AD są równoległe. ABCD– jest zatem trapezem

Zadanie 1
143Zadanie 2
143Zadanie 3
143Zadanie 6
143Zadanie 7
144Zadanie 12
144Zadanie 13
145Zadanie 14
145Zadanie 15
145Zadanie 17
145Zadanie 6
149Zadanie 11
150Ćwiczenie B
51Zadanie 1
155Zadanie 2
155Zadanie 7
156Zadanie 8
156Zadanie 11
156Zadanie 14
157Zadanie 16
157Zadanie 23
158Ćwiczenie B
160Zadanie 1
162Zadanie 2
162Zadanie 5
163Zadanie 6
162Zadanie 7
163Zadanie 8
163Zadanie 7
169Zadanie 8
169Zadanie 15
169Ćwiczenie A
170Zadanie 1
162Zadanie 4
174Zadanie 5
174Zadanie 6
174Zadanie 7
174Zadanie 8
174Zadanie 10
162Zadanie 11
162Zadanie 12
174Zadanie 13
175Zadanie 16
175Zadanie 18
176Zadanie 20
176Zadanie 22
176Zadanie 23
177Zadanie 24
177Zadanie 26
177Zadanie 3
178Zadanie 10
178Zadanie 11
178
