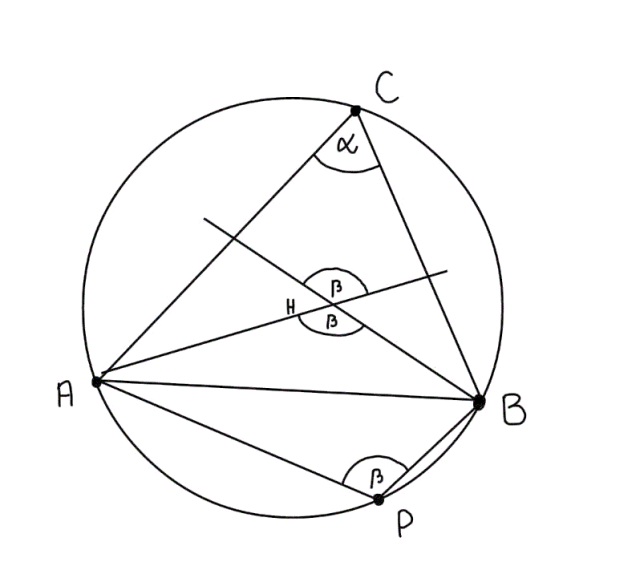
W tym zadaniu, wiedząc, że punkt P jest symetryczny do ortocentrum ( punkt przecięcia się wszystkich wysokości trójkąta ) udowodnij, że leży on na okręgu opisanym na trójkącie ABC.
![]()
![]()
![]()
![]()
Okrąg opisany na trójkącie ABC jest również okręgiem opisanym na czworokącie APBC.

Trójkąty APB oraz AHB są przystające na podstawie cechy bok-bok-bok.
Pamiętaj, że suma miar kątów wewnętrznych wynosi 360°.
Przyjmij oznaczenia jak na rysunku

Zadanie 1
143Zadanie 2
143Zadanie 3
143Zadanie 6
143Zadanie 7
144Zadanie 12
144Zadanie 13
145Zadanie 14
145Zadanie 15
145Zadanie 17
145Zadanie 6
149Zadanie 11
150Ćwiczenie B
51Zadanie 1
155Zadanie 2
155Zadanie 7
156Zadanie 8
156Zadanie 11
156Zadanie 14
157Zadanie 16
157Zadanie 23
158Ćwiczenie B
160Zadanie 1
162Zadanie 2
162Zadanie 5
163Zadanie 6
162Zadanie 7
163Zadanie 8
163Zadanie 7
169Zadanie 8
169Zadanie 15
169Ćwiczenie A
170Zadanie 1
162Zadanie 4
174Zadanie 5
174Zadanie 6
174Zadanie 7
174Zadanie 8
174Zadanie 10
162Zadanie 11
162Zadanie 12
174Zadanie 13
175Zadanie 16
175Zadanie 18
176Zadanie 20
176Zadanie 22
176Zadanie 23
177Zadanie 24
177Zadanie 26
177Zadanie 3
178Zadanie 10
178Zadanie 11
178
