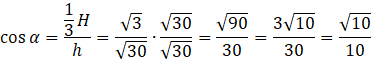
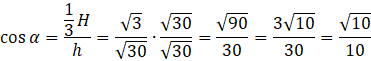
ODP: Pole powierzchni bocznej wynosi
, a cosinus kąta znajdującego się pomiędzy wysokością ściany bocznej i płaszczyzna podstawy jest równy
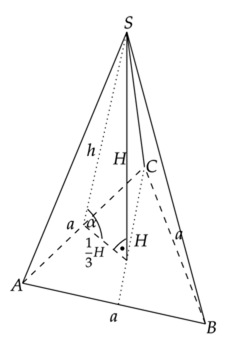
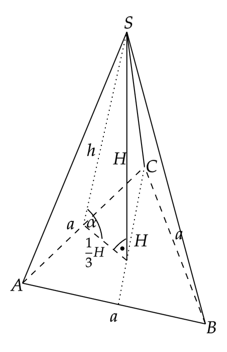
Wykonaj rysunek pomocniczy:
Pod wzór na objętość podstaw znane wartości. Zauważ, że podstawa jest trójkątem równobocznym, więc znasz wzór na jego pole.
Z powyższego równania wyznacz wartość
Oblicz długość wysokości ostrosłupa.
Zauważ, że wysokość ściany bocznej, wysokość ostrosłupa i trzecia część wysokości podstawy tworzą trójkąt prostokątny. Skorzystaj z twierdzenia Pitagorasa i oblicz długość pierwszej z wysokości.
Zauważ, że pole boczne ostrosłupa składa się z trzech trójkątów o podstawie długości 6 i wysokości
Na tej podstawie je oblicz.
Oblicz cosinus kąta pomiędzy ścianą boczną, a krawędzią podstawy ostrosłupa. Zauważ, że jest to iloraz trzeciej część wysokości podstawy i wysokości ściany bocznej.
