![]()
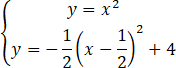
![]()
![]()
![]()
![]()
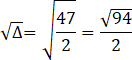
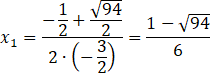
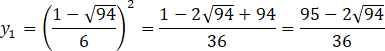
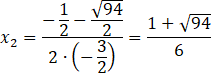
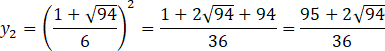
![]()
![]()
![]()
![]()
![]()
![]()
Punkt K leży na prostej
![]() , więc
, więc
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – największa wartość pochodnej
– największa wartość pochodnej
![]()
![]()
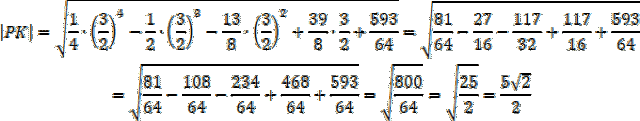
ODP:
![]() ,
,
![]()

Wyznacz współrzędne punktów przecięcia prostych
![]() i
i
![]() .
.
![]()
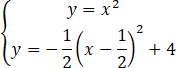
Skorzystaj z metody podstawienia i podstaw wartość
![]() z pierwszego równania pod drugie.
z pierwszego równania pod drugie.
![]()
Wyznacz rozwiązania powstałego równania. Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
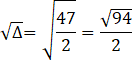
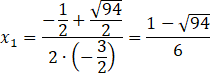
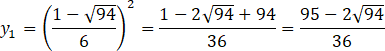
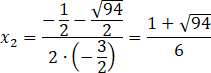
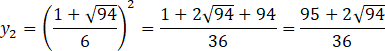
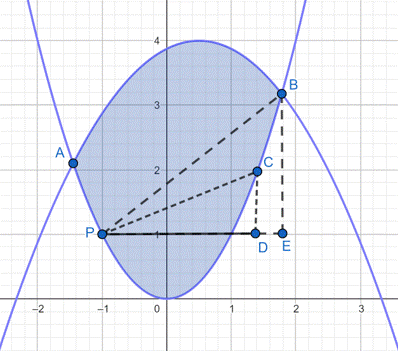
Zapisz współrzędne punktów A i B, wyznaczających przecięcia wykresów funkcji.
![]()
Zaznacz na wykresie funkcji
![]() punkt C oraz na wykresie funkcji
punkt C oraz na wykresie funkcji
![]() punkt B. Dodatkowo oznacz na wykresie punkty D i E tak, aby utworzone trójkąty CDP i BEP były prostokątne.
punkt B. Dodatkowo oznacz na wykresie punkty D i E tak, aby utworzone trójkąty CDP i BEP były prostokątne.
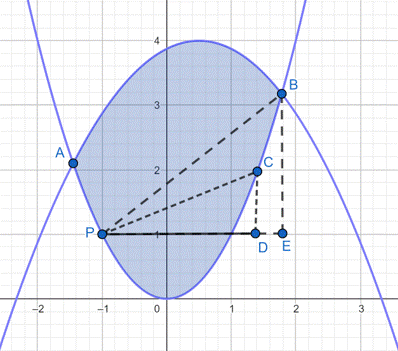
Zauważ, że przyprostokątne trójkąta CDP są krótsze od przyprostokątnych trójkąta BEP.
![]()
![]()
Dodaj obustronnie.
![]()
Skorzystaj z twierdzenia Pitagorasa w powstałej nierówności.
![]()
![]()
Oznacza to, że aby odległość z punktu P do punktu K była największa, to musi on leżeć na wykresie funkcji
![]() . Możesz więc skorzystać ze wzoru na odległość pomiędzy punktem P, a punktem leżącym na wykresie funkcji
. Możesz więc skorzystać ze wzoru na odległość pomiędzy punktem P, a punktem leżącym na wykresie funkcji
![]() .
.
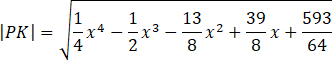
Wprowadź równanie funkcji pomocniczej, aby pozbyć się pierwiastka.
![]()
Zapisz dziedzinę tej funkcji. Zauważ, że szukany punkt K znajduję się pomiędzy punktami A i B.
![]()
Wyznacz równanie pochodnej funkcji
![]() i oblicz jej miejsca zerowe.
i oblicz jej miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
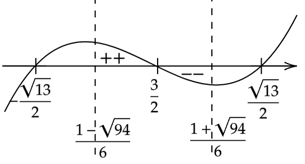
Zauważ, że tylko jedno z trzech wyliczonych miejsc należy do dziedziny.
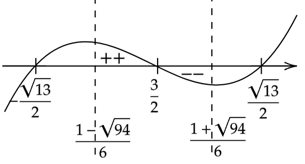
Oznacza to, że pochodna w przedziale
![]() ma jedno miejsce zerowe
ma jedno miejsce zerowe
![]() i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
![]() (oraz
(oraz
![]() ) rośnie w przedziale
) rośnie w przedziale
![]() ,a maleje w przedziale
,a maleje w przedziale
![]() . Więc będzie to największa wartość pochodnej.
. Więc będzie to największa wartość pochodnej.
Oblicz współrzędne punktu K oraz jego odległość do punku P.
![]()
![]()
