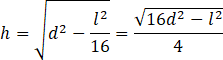
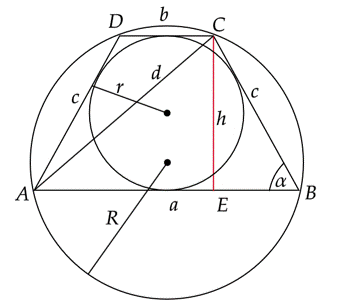
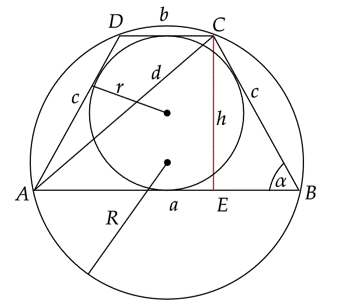
Wykaż, że promień $\text{[math]}$ okręgu opisanego na trapezie równoramiennym $\text{[math]}$ o obwodzie $\text{[math]}$ , w którym $\text{[math]}$ , a przekątna $\text{[math]}$ ma długość $\text{[math]}$ jest równy $\text{[math]}$ .

$\text{[math]}$

Trójkąt ABC jest wpisany w okrąg.

$\text{[math]}$

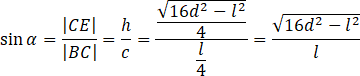
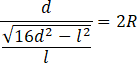
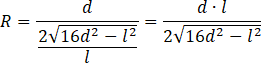
Wprowadź oznaczenia pomocnicze:

Z treści zadania wiesz, że obwód trapezu ABCD wynosi $\text{[math]}$ . Zapisz to za pomocą wyrażenia algebraicznego.

$\text{[math]}$

Skorzystaj z tego, że skoro w czworokąt jest wpisany okrąg, więc suma jego przeciwległych boków jest równa.

$\text{[math]}$

Podstaw wartość $\text{[math]}$ pod równanie z obwodem.

$\text{[math]}$

Wyznacz wartość $\text{[math]}$ .

$\text{[math]}$

Zapisz długość odcinka AE.

$\text{[math]}$

Skorzystaj z twierdzenia Pitagorasa w trójkącie ACE i wyznacz z niego długość wysokości $\text{[math]}$ .

$\text{[math]}$

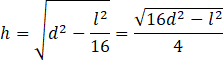
Zauważ, że trójkąt ABC jest wpisany w okrąg o takim samym promieniu jak trapez ABCD. Na tej podstawie skorzystaj z twierdzenia sinusów w tym trójkącie.

$\text{[math]}$

Oblicz wartość sinusa kąta $\text{[math]}$ .

$\text{[math]}$

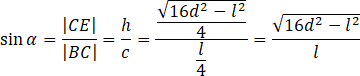
Podstaw obliczony sinus pod równanie zawierające twierdzenie sinusów i wyznacz z niego długość promienia $\text{[math]}$ .

$\text{[math]}$

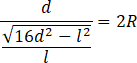
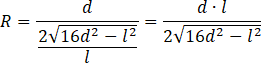
To kończy dowód.

Ćwiczenie 5., strona 74, Matematyka wokół nas. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 1., strona 64, Matematyka z plusem. Liczby naturalne. Klasa 4. Zeszyt ćwiczeń. Wersja A. Część 1/3 - rozwiązania i odpowiedzi

Zadanie 13, strona 59, Matematyka z kluczem. Klasa 4. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 30., strona 219, Matematyka. Klasa 1. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 19, strona 8, Matura z matematyki. Poziom podstawowy. 2018

Zadanie 48., strona 370, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 2.14., strona 326, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 54., strona 190, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 2., strona 194, Matematyka. Klasa 3. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 73., strona 417, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 6

Matura z matematyki. Arkusz pokazowy. Poziom rozszerzony. 2023

Zadanie 8 - strona 20

Zadanie

Wykaż, że promień $\text{[math]}$ okręgu opisanego na trapezie równoramiennym $\text{[math]}$ o obwodzie $\text{[math]}$ , w którym $\text{[math]}$ , a przekątna $\text{[math]}$ ma długość $\text{[math]}$ jest równy $\text{[math]}$ .

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania

Zadania przypisane do działu

Matura z matematyki. Arkusz pokazowy. Poziom rozszerzony. 2023

Zadanie 8 - strona 20

Zadanie

Wykaż, że promień okręgu opisanego na trapezie równoramiennym o obwodzie , w którym , a przekątna ma długość jest równy .

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania

Zadania przypisane do działu

Wykaż, że promień $\text{[math]}$ okręgu opisanego na trapezie równoramiennym $\text{[math]}$ o obwodzie $\text{[math]}$ , w którym $\text{[math]}$ , a przekątna $\text{[math]}$ ma długość $\text{[math]}$ jest równy $\text{[math]}$ .