![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP:
![]()

Zauważ, że równanie
![]() jest równe zero, gdy któryś z nawiasów zeruję się.
jest równe zero, gdy któryś z nawiasów zeruję się.
![]()
Oblicz dla jakiego
![]() pierwsze równanie zeruję się.
pierwsze równanie zeruję się.
![]()
![]()
Oznacza to, że jednym z rozwiązań równania
![]() jest
jest
![]() . Więc rozwiązania równania
. Więc rozwiązania równania
![]() muszą być dodatnie.
muszą być dodatnie.
Zapisz jakie warunki musi spełniać równanie
![]() aby
aby
![]() miało trzy różne równania o takim samym znaku.
miało trzy różne równania o takim samym znaku.
![]() – aby równanie było kwadratowe, to współczynnik kierunkowy nie może być zerem,
– aby równanie było kwadratowe, to współczynnik kierunkowy nie może być zerem,
![]() – równanie ma dwa miejsca zerowe, gdy delta jest większa od zera,
– równanie ma dwa miejsca zerowe, gdy delta jest większa od zera,
![]() – iloczyn rozwiązań musi być większy od zera,
– iloczyn rozwiązań musi być większy od zera,
![]() – suma rozwiązań musi być dodatnia,
– suma rozwiązań musi być dodatnia,
![]() – rozwiązania równania
– rozwiązania równania
![]() nie mogą być równe rozwiązaniu równania
nie mogą być równe rozwiązaniu równania
![]() .
.
Oblicz dla jakich
![]() spełniony jest pierwszy warunek.
spełniony jest pierwszy warunek.
![]()
![]()
Oblicz dla jakich
![]() spełniony jest drugi warunek, czyli delta jest większa od zera.
spełniony jest drugi warunek, czyli delta jest większa od zera.
![]()
![]()
Oblicz deltę z delty i rozwiązania nierówności.
![]()
![]()
![]()
![]()
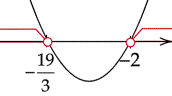
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest nad osią.
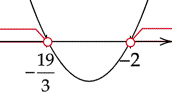
![]()
Oblicz dla jakich
![]() spełniony jest trzeci warunek, czyli iloczyn rozwiązań jest większy od zera. Skorzystaj z wzorów Viete’a.
spełniony jest trzeci warunek, czyli iloczyn rozwiązań jest większy od zera. Skorzystaj z wzorów Viete’a.
![]()
![]()
![]()
Pomnóż całą nierówność przez kwadrat mianownika, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
![]()
Oblicz dla jakich
![]() nierówność się zeruje.
nierówność się zeruje.
![]()
![]()
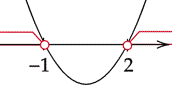
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest nad osią.
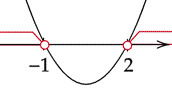
![]()
Oblicz dla jakich
![]() spełniony jest czwarty warunek, czyli suma rozwiązań jest większa od zera. Skorzystaj z wzorów Viete’a.
spełniony jest czwarty warunek, czyli suma rozwiązań jest większa od zera. Skorzystaj z wzorów Viete’a.
![]()
![]()
![]()
Pomnóż całą nierówność przez kwadrat mianownika, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
![]()
Oblicz dla jakich
![]() nierówność się zeruje.
nierówność się zeruje.
![]()
![]()
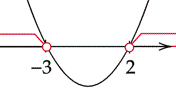
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest nad osią.
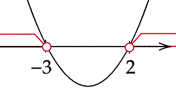
![]()
Oblicz dla jakich
![]() spełniony jest piąty warunek, czyli miejsca zerowe są różne od 6. Aby to obliczyć, podstaw w miejsce
spełniony jest piąty warunek, czyli miejsca zerowe są różne od 6. Aby to obliczyć, podstaw w miejsce
![]() wartość 6.
wartość 6.
![]()
![]()
![]()
![]()
![]()
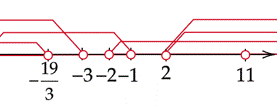
Zaznacz na osi wszystkie obliczone powyżej przedziały. Rozwiązaniem będzie ich część wspólna.
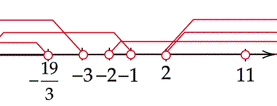
![]()