1.
![]()
2.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
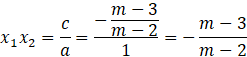
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP: Rozwiązaniem zadania są
![]() należące do przedziału
należące do przedziału
![]()

Zauważ, że aby równanie miało dwa rozwiązania i spełniało warunek podany w treści zadania, to:
1.
![]()
2.
![]()
Oblicz dla jakich
![]() spełniony jest pierwszy warunek, czyli delta jest większa od zera.
spełniony jest pierwszy warunek, czyli delta jest większa od zera.
![]()
![]()
Pomnóż całą nierówność przez kwadrat mianownika znajdującego się z lewej strony nierówności, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
![]()
Wymnóż powstałe nawiasy, skorzystaj ze wzoru skróconego mnożenia na kwadrat różnicy:
![]() i dokonaj redukcji jednomianów podobnych.
i dokonaj redukcji jednomianów podobnych.
![]()
![]()
![]()
Oblicz deltę z delty i rozwiązania powstałej nierówności.
![]()
![]()
![]()
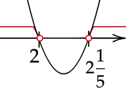
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest nad osią. Ramiona paraboli skieruj do góry, ponieważ współczynnik stojący przy
![]() z największą potęgą jest dodatni.
z największą potęgą jest dodatni.
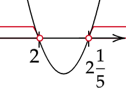
Oblicz dla jakich
![]() spełniony jest drugi warunek, czyli
spełniony jest drugi warunek, czyli
![]() .
.
Skorzystaj ze wzoru skróconego mnożenia na sumę sześcianów:
![]() .
.
![]()
Przekształć drugi nawias w powyższej nierówności do otrzymania postaci ze wzorami Viete’a, czyli sumy miejsc zerowych lub ich iloczynu. Skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy:
![]()
![]()
![]()
Zastosuj wzory Viete’a do powyższej nierówności.
![]()
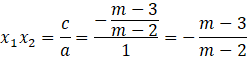
Wymnóż nawiasy, przemieś wszystkie wartości na lewą stronę i przekształć nierówność do uzyskania najprostszej postaci.
![]()
![]()
![]()
Pomnóż całą nierówność przez kwadrat mianownika znajdującego się z lewej strony nierówności, ponieważ nie wiadomo czy jest on liczbą dodatnią czy ujemną, a mnożąc przez kwadrat jakiejkolwiek liczby masz pewność, że jest to liczba dodatnia i znak nierówności nie zmieni się.
![]()
![]()
Wyłącz wspólny czynnik przed nawias.
![]()
![]()
![]()
Zauważ, że powyższa nierówność jest równa zero, gdy któryś z nawiasów zeruję się.
![]()
Rozwiąż rozwiązania każdego z nawiasów.
![]()
![]()
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest pod osią. Ramiona paraboli skieruj do góry, ponieważ współczynnik stojący przy
![]() z największą potęgą jest dodatni.
z największą potęgą jest dodatni.
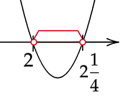
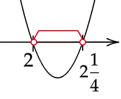
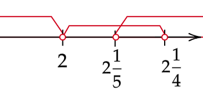
Zaznacz na osi wszystkie obliczone powyżej przedziały. Rozwiązaniem będzie ich część wspólna.
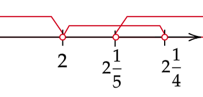
![]()