![]()
![]()
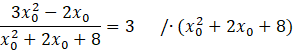
![]()
![]()
![]()
![]()
![]()
![]()
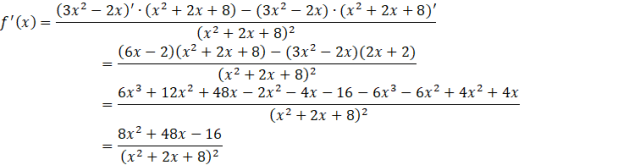
![]()
![]()
ODP: Pierwszą współrzędną punktu
![]() jest
jest
![]() Styczna do wykresu funkcji
Styczna do wykresu funkcji
![]() w punkcie
w punkcie
![]() ma równanie
ma równanie
![]() .
.

Z treści zadania wiesz, że
![]() , więc nie musisz wyznaczać dziedziny funkcji
, więc nie musisz wyznaczać dziedziny funkcji
![]() .
.
![]()
Zauważ, że skoro punkt
![]() należy do wykresu funkcji
należy do wykresu funkcji
![]() , to w miejsce
, to w miejsce
![]() możesz podstawić wartość
możesz podstawić wartość
![]() , a w miejsce
, a w miejsce
![]() wartość
wartość
![]() , czyli obliczyć:
, czyli obliczyć:
![]()
Z powstałego równania wyznacz wartość
![]() . Pomnóż całe równanie przez mianownik znajdujący się z lewej strony równania.
. Pomnóż całe równanie przez mianownik znajdujący się z lewej strony równania.
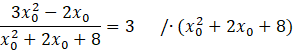
Wymnóż powstały nawias i zredukuj jednomiany podobne.
![]()
![]()
![]()
![]()
Zauważ, że znasz już obie współrzędne punktu
![]() . Ponieważ musisz wyznaczyć równanie stycznej do wykresu funkcji
. Ponieważ musisz wyznaczyć równanie stycznej do wykresu funkcji
![]() w punkcie
w punkcie
![]() możesz go oznaczyć jako:
możesz go oznaczyć jako:
![]()
Zapisz wzór na równanie stycznej do wykresu:
![]()
Zauważ, że aby obliczyć współczynnik kierunkowy szukanej stycznej musisz obliczyć pochodną funkcji
![]() . Wymnóż powstałe nawiasy, dokonaj redukcji jednomianów podobnych i przedstaw ją w najprostszej postaci.
. Wymnóż powstałe nawiasy, dokonaj redukcji jednomianów podobnych i przedstaw ją w najprostszej postaci.
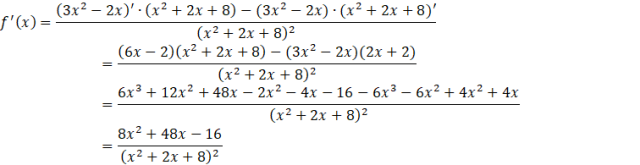
Oblicz wartość pochodnej funkcji dla pierwszej współrzędnej punktu
![]() , czyli
, czyli
![]()
![]()
Pod wzór na równanie stycznej podstaw znane wartości i przedstaw wzór szukanej prostej w najprostszej postaci.
![]()