![]()
![]()
![]()
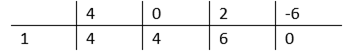
![]()
![]()
![]() – brak rozwiązań
– brak rozwiązań
![]()
![]()
ODP: Najmniejsza wartość funkcji
![]() wynosi
wynosi
![]()

![]()
Oblicz pochodną funkcji
![]() .
.
![]()
Zauważ, że liczba 1 jest miejscem zerowym pochodnej funkcji, ponieważ:
![]()
Skorzystaj ze schematu Hornera. Narysuj tabelę. W pierwszym wierszu wpisz wszystkie kolejne współczynniki uporządkowanej pochodnej funkcji
![]() . W lewym dolnym rogu najniższego wiersza tabelki wpisz liczbę, która jest jej miejscem zerowym, czyli 1. Przepisz pierwszy współczynnik bez zmian do dolnego wiersza. Tak otrzymaną liczbę 4 pomnóż przez liczbę 1, następnie dodaj liczbę 0. Wynik będący liczbą 4 wpisz do kolejnej komórki dolnego wiersza w schemacie Hornera. Podobnie postępuj z kolejnymi współczynnikami wielomianu.
. W lewym dolnym rogu najniższego wiersza tabelki wpisz liczbę, która jest jej miejscem zerowym, czyli 1. Przepisz pierwszy współczynnik bez zmian do dolnego wiersza. Tak otrzymaną liczbę 4 pomnóż przez liczbę 1, następnie dodaj liczbę 0. Wynik będący liczbą 4 wpisz do kolejnej komórki dolnego wiersza w schemacie Hornera. Podobnie postępuj z kolejnymi współczynnikami wielomianu.
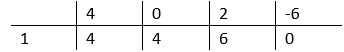
Liczby powstałe w dolnym wierszu są współczynnikami trójmianu. Zapisz wzór pochodnej funkcji za pomocą iloczynu dwóch powyższych nawiasów.
![]()
Oblicz pozostałe miejsca zerowe pochodnej funkcji
![]() . Zauważ, że powyższa nierówność jest równa zero, gdy któryś z nawiasów zeruję się. Rozwiązanie pierwszego nawiasu już znasz. Oblicz deltę drugiego nawiasu, aby wyznaczyć jego rozwiązania.
. Zauważ, że powyższa nierówność jest równa zero, gdy któryś z nawiasów zeruję się. Rozwiązanie pierwszego nawiasu już znasz. Oblicz deltę drugiego nawiasu, aby wyznaczyć jego rozwiązania.
![]()
![]() – delta jest mniejsza od zera, więc równanie nie ma rozwiązań
– delta jest mniejsza od zera, więc równanie nie ma rozwiązań
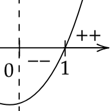
Zaznacz uzyskane miejsca zerowe na osi. Pamiętaj o uwzględnieniu dziedziny.
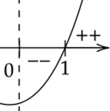
Oznacza to, że pochodna w przedziale
![]() ma jedno miejsce zerowe
ma jedno miejsce zerowe
![]() i zmienia w tym punkcie znak z ujemnego na dodatni. W takim razie funkcja
i zmienia w tym punkcie znak z ujemnego na dodatni. W takim razie funkcja
![]() i jednocześnie
i jednocześnie
![]() maleje w przedziale
maleje w przedziale
![]() , a rośnie w przedziale
, a rośnie w przedziale
![]() . Więc będzie to najmniejsza wartość pochodnej:
. Więc będzie to najmniejsza wartość pochodnej:
![]()
Oblicz najmniejszą wartość funkcji
![]() . Aby to zrobić oblicz wartość
. Aby to zrobić oblicz wartość
![]()
![]()