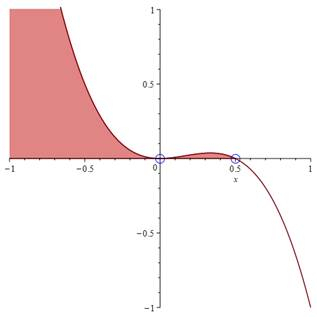
W tym zadaniu musisz zbadać, czy istnieje parametr, dla którego suma sześcianów dwóch różnych rozwiązań równania kwadratowego jest najmniejsza.
nie istnieje

Funkcja kwadratowa ma dwa różne pierwiastki wtedy i tylko wtedy, gdy:
![]()
![]()
![]()
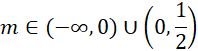
Niech
![]() oraz
oraz
![]() oznaczają pierwiastki tego wielomianu kwadratowego. Zauważ, że:
oznaczają pierwiastki tego wielomianu kwadratowego. Zauważ, że:
![]()
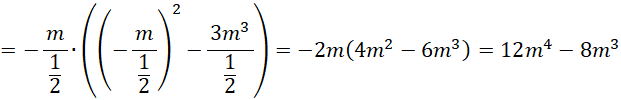
Korzystasz tutaj ze wzorów Viete’a dla wielomianu kwadratowego postaci:
![]()
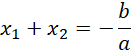
![]()
Zapisz ten wynik jako funkcję od zmiennej m:
![]()
Oblicz pochodną w celu znalezienia punktu krytycznego:
![]()
![]()
![]()
![]()
![]()
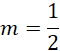
Dla
![]() masz
masz
![]() a to ma jeden pierwiastek podwójny, dlatego jest sprzeczne z założeniami zadania. Dodatkowo
a to ma jeden pierwiastek podwójny, dlatego jest sprzeczne z założeniami zadania. Dodatkowo
![]() nie należy do pożądanego przedziału, stąd sprawdzasz wartości na krańcach przedziałów:
nie należy do pożądanego przedziału, stąd sprawdzasz wartości na krańcach przedziałów:
![]()
![]()
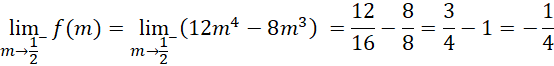
Stąd nie istnieje takie, dla którego
![]() suma sześcianów dwóch różnych pierwiastków równania byłaby najmniejsza.
suma sześcianów dwóch różnych pierwiastków równania byłaby najmniejsza.

Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 4.
288Zadanie 1.
292Zadanie 2.
288Zadanie 3.
292Zadanie 1.
296Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 1.
300Zadanie 2.
300Zadanie 3.
300Zadanie 4.
300Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Ćwiczenie 1.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
306Zadanie 4.
306Zadanie 5.
306Zadanie 1.
311Zadanie 2.
311Zadanie 3.
311Zadanie 1.
319Zadanie 3.
319Ćwiczenie 3.
323Zadanie 1.
326Zadanie 2.
326Zadanie 3.
326Zadanie 4.
326Zadanie 1.
335Zadanie 2.
335Zadanie 3.
335Zadanie 4.
335Ćwiczenie 2.
342Zadanie 1.
344Zadanie 2.
344Zadanie 3.
344Zadanie 4.
344Zadanie 5.
344Zadanie 6.
344Ćwiczenie 2.
349Zadanie 1.
352Zadanie 2.
352Zadanie 3.
352Zadanie 4.
352Zadanie 7.
352Zadanie 5.
363Zadanie 6.
363Zadanie 7.
363Zadanie 8.
363Ćwiczenie 2.
370Zadanie 1.
372Zadanie 4.
373Zadanie 5.
373Zadanie 6.
373Zadanie 8.
373Zadanie 12.
373Ćwiczenie 2.
376Zadanie 1.
379Zadanie 2.
379Zadanie 4.
379Zadanie 5.
379Zadanie 14.
389Zadanie 18.
389Zadanie 19.
389Zadanie 20.
389
