W tym zadaniu musisz obliczyć granicę funkcji, korzystając z definicji Heinego.
![]()
Funkcja jest określona na całym zbiorze liczb rzeczywistych. Weź dowolny ciąg
![]() , o wyrazach należących do sąsiedztwa
, o wyrazach należących do sąsiedztwa
![]() i zbieżny do -2,
i zbieżny do -2,
![]() . Wówczas:
. Wówczas:
![]()
Granica
![]() istnieje i
istnieje i
![]()
![]()
![]()
Zatem
![]()

Sąsiedztwo
![]() określamy jako zbiór
określamy jako zbiór
![]() dla
dla
![]() . Definicja Heinego:
. Definicja Heinego:
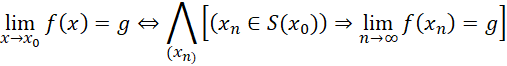

Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 4.
288Zadanie 1.
292Zadanie 2.
288Zadanie 3.
292Zadanie 1.
296Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 1.
300Zadanie 2.
300Zadanie 3.
300Zadanie 4.
300Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Ćwiczenie 1.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
306Zadanie 4.
306Zadanie 5.
306Zadanie 1.
311Zadanie 2.
311Zadanie 3.
311Zadanie 1.
319Zadanie 3.
319Ćwiczenie 3.
323Zadanie 1.
326Zadanie 2.
326Zadanie 3.
326Zadanie 4.
326Zadanie 1.
335Zadanie 2.
335Zadanie 3.
335Zadanie 4.
335Ćwiczenie 2.
342Zadanie 1.
344Zadanie 2.
344Zadanie 3.
344Zadanie 4.
344Zadanie 5.
344Zadanie 6.
344Ćwiczenie 2.
349Zadanie 1.
352Zadanie 2.
352Zadanie 3.
352Zadanie 4.
352Zadanie 7.
352Zadanie 5.
363Zadanie 6.
363Zadanie 7.
363Zadanie 8.
363Ćwiczenie 2.
370Zadanie 1.
372Zadanie 4.
373Zadanie 5.
373Zadanie 6.
373Zadanie 8.
373Zadanie 12.
373Ćwiczenie 2.
376Zadanie 1.
379Zadanie 2.
379Zadanie 4.
379Zadanie 5.
379Zadanie 14.
389Zadanie 18.
389Zadanie 19.
389Zadanie 20.
389
