W tym zadaniu musisz wykazać nierówność dla funkcji.
![]()
![]()
Zapisz wyrażenia po lewej stronie nierówności jako funkcję od zmiennej x:
![]()
Oblicz pochodną tej funkcji:
![]()
![]()
Czyli dla
![]() :
:
![]()
![]()
![]()
Co należało wykazać.

Zauważ, że pochodna tej funkcji dla
![]() jest zawsze dodatnia. Wynika to stąd, że:
jest zawsze dodatnia. Wynika to stąd, że:
![]()
![]()
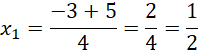
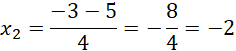
Czyli dla
![]() to równanie kwadratowe przyjmuje wartości większe od zera.
to równanie kwadratowe przyjmuje wartości większe od zera.
Stąd funkcja jest rosnąca na całym tym przedziale. Zatem jeżeli dla
![]() (chociaż ten punkt nie należy do dziedziny funkcji, możesz policzyć wartość dla tego punktu z ciągłości funkcji wielomianowej) funkcja jest większa lub równa zero, to dla wszystkich pozostałych x-ów z przedziału
(chociaż ten punkt nie należy do dziedziny funkcji, możesz policzyć wartość dla tego punktu z ciągłości funkcji wielomianowej) funkcja jest większa lub równa zero, to dla wszystkich pozostałych x-ów z przedziału
![]() funkcja ta będzie większa od zera (w przeciwnym razie ta funkcja nie byłaby rosnąca).
funkcja ta będzie większa od zera (w przeciwnym razie ta funkcja nie byłaby rosnąca).

Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 4.
288Zadanie 1.
292Zadanie 2.
288Zadanie 3.
292Zadanie 1.
296Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 1.
300Zadanie 2.
300Zadanie 3.
300Zadanie 4.
300Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Ćwiczenie 1.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
306Zadanie 4.
306Zadanie 5.
306Zadanie 1.
311Zadanie 2.
311Zadanie 3.
311Zadanie 1.
319Zadanie 3.
319Ćwiczenie 3.
323Zadanie 1.
326Zadanie 2.
326Zadanie 3.
326Zadanie 4.
326Zadanie 1.
335Zadanie 2.
335Zadanie 3.
335Zadanie 4.
335Ćwiczenie 2.
342Zadanie 1.
344Zadanie 2.
344Zadanie 3.
344Zadanie 4.
344Zadanie 5.
344Zadanie 6.
344Ćwiczenie 2.
349Zadanie 1.
352Zadanie 2.
352Zadanie 3.
352Zadanie 4.
352Zadanie 7.
352Zadanie 5.
363Zadanie 6.
363Zadanie 7.
363Zadanie 8.
363Ćwiczenie 2.
370Zadanie 1.
372Zadanie 4.
373Zadanie 5.
373Zadanie 6.
373Zadanie 8.
373Zadanie 12.
373Ćwiczenie 2.
376Zadanie 1.
379Zadanie 2.
379Zadanie 4.
379Zadanie 5.
379Zadanie 14.
389Zadanie 18.
389Zadanie 19.
389Zadanie 20.
389
