W tym zadaniu musisz wyznaczyć zbiór wartości funkcji.
![]()

Polic granice w zerze:
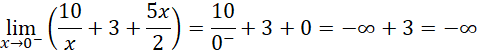
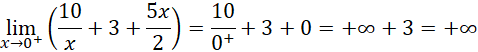
Sprawdź, czy funkcja nie ma ekstremów lokalnych:
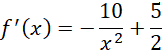
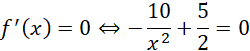
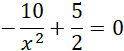
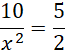
![]()
![]()
![]()
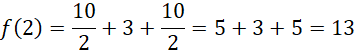
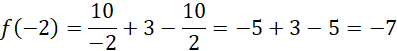
Z ciągłości w przedziałach wnioskujesz, że zbiór wartości tej funkcji wynosi:
![]()

Zadanie 1.
288Zadanie 2.
288Zadanie 3.
288Zadanie 4.
288Zadanie 1.
292Zadanie 2.
288Zadanie 3.
292Zadanie 1.
296Zadanie 2.
296Zadanie 3.
296Zadanie 4.
296Zadanie 1.
300Zadanie 2.
300Zadanie 3.
300Zadanie 4.
300Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Ćwiczenie 1.
302Ćwiczenie 2.
304Ćwiczenie 3.
305Zadanie 1.
306Zadanie 2.
306Zadanie 3.
306Zadanie 4.
306Zadanie 5.
306Zadanie 1.
311Zadanie 2.
311Zadanie 3.
311Zadanie 1.
319Zadanie 3.
319Ćwiczenie 3.
323Zadanie 1.
326Zadanie 2.
326Zadanie 3.
326Zadanie 4.
326Zadanie 1.
335Zadanie 2.
335Zadanie 3.
335Zadanie 4.
335Ćwiczenie 2.
342Zadanie 1.
344Zadanie 2.
344Zadanie 3.
344Zadanie 4.
344Zadanie 5.
344Zadanie 6.
344Ćwiczenie 2.
349Zadanie 1.
352Zadanie 2.
352Zadanie 3.
352Zadanie 4.
352Zadanie 7.
352Zadanie 5.
363Zadanie 6.
363Zadanie 7.
363Zadanie 8.
363Ćwiczenie 2.
370Zadanie 1.
372Zadanie 4.
373Zadanie 5.
373Zadanie 6.
373Zadanie 8.
373Zadanie 12.
373Ćwiczenie 2.
376Zadanie 1.
379Zadanie 2.
379Zadanie 4.
379Zadanie 5.
379Zadanie 14.
389Zadanie 18.
389Zadanie 19.
389Zadanie 20.
389
