Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 12 - strona 12

Oblicz dla jakiego m trójmian kwadratowy $\text{[math]}$ ma dwa różne pierwiastki $\text{[math]}$ tego samego znaku, spełniające warunek $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

ODP: $\text{[math]}$

Równanie ma dwa rozwiązania wtedy gdy delta jest większa od zera. Oblicz dla jakich m: $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Oblicz dla jakiego m każdy z nawiasów się zeruje.

$\text{[math]}$

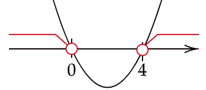
Zapisz powyższe rozwiązania na osi. Ramiona paraboli skieruj do góry. Zaznacz dla jakich x parabola jest nad osią.

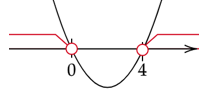
Zapisz zaznaczony przedział nierówności.

$\text{[math]}$

Przekształć równanie 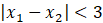$\text{[math]}$ do otrzymania postaci ze wzorami Viete’a. Podnieś obie strony nierówności do kwadratu.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy.

$\text{[math]}$

Zastosuj wzory Viete’a do powyższego równania.

$\text{[math]}$

$\text{[math]}$

Podstaw wyliczone wzory. Doprowadź nierówność do najprostszej postaci.

$\text{[math]}$

$\text{[math]}$

Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

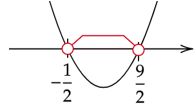
Zapisz powyższe rozwiązania na osi. Ramiona paraboli skieruj do góry. Zaznacz dla jakich x parabola jest pod osią.

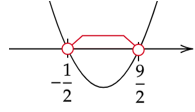
Zapisz zaznaczony przedział nierówności.

$\text{[math]}$

Zauważ, że jeśli oba pierwiastki mają być tego samego znaku, to ich iloczyn będzie zawsze dodatni.

$\text{[math]}$

Zastosuj wzory Viete’a do powyższego równania.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

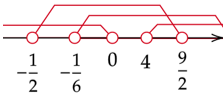
Zapisz wszystkie rozwiązania na osi.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

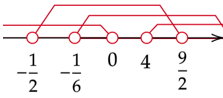
Zapisz część wspólną wszystkich zbiorów. Będzie to szukany przedział m.

$\text{[math]}$

Zadanie 6, strona 236, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1., strona 212, To się liczy! Klasa 1. Podręcznik – rozwiązania i odpowiedzi

Zadanie 3, strona 186, Matematyka. Klasa 4. Podręcznik - rozwiązania i odpowiedzi

Zadanie 75., strona 83, Matematyka z plusem. Klasa 2. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 16, strona 54, Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Ćwiczenie 8., strona 107, Matematyka. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie zestaw 1 7., strona 386, Matematyka. Klasa 1. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie Super zagadka, strona 190, Matematyka z plusem. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie 13., strona 126, Matematyka z kluczem. Klasa 5. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 6, strona 121, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

2

2

2

2

4

4

5

6

8

10

11

12

14

16

18

20

Pełny spis treści