Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 14, a) - strona 35

Oblicz liczby $\text{[math]}$ . Podaj dziedzinę funkcji $\text{[math]}$ oraz dziedzinę funkcji $\text{[math]}$ , jeśli wykresy funkcji $\text{[math]}$ i $\text{[math]}$ przecinają oś OY w punkcie o rzędnej 2.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

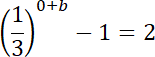
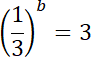
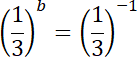
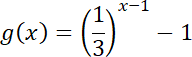
Podstaw współrzędne podane punktu pod wzór funkcji $\text{[math]}$ i $\text{[math]}$ . Następnie z powstałych równań wyznacz wartości współczynników $\text{[math]}$ i $\text{[math]}$ .

Na koniec wyznacz dziedzinę każdej z funkcji. Skorzystaj z tego, że dla logarytmu $\text{[math]}$ liczba logarytmowana $\text{[math]}$ musi być większa od 0, a w wykładniku potęgi $\text{[math]}$ może być dowolna liczba.

Zadanie 3, strona 177, Matematyka z kluczem. Klasa 6. Podręcznik. Część 2 - rozwiązania i odpowiedzi

Ćwiczenie 2., strona 248, Matematyka. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 2.54., strona 49, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 6., strona 466, Matematyka. Klasa 3. Zakres rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie 14.23., strona 314, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie 16, strona 277, Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 4., strona 162, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Ćwiczenie 10, strona 30, Matematyka z kluczem. Klasa 5. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 18, strona 219, NOWA MATeMAtyka 1. Podręcznik. Zakres podstawowy i rozszerzony

Ćwiczenie 3, strona 10, Matematyka z kluczem. Klasa 5. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 2.1

23

23

23

23

23

23

23

23

23

Zadanie 2.2

23

23

23

23

23

23

23

23

23

Zadanie 2.3

23

23

23

23

23

23

23

Zadanie 2.4

23

23

23

23

23

23

23

Zadanie 2.5

23

23

23

23

23

23

23

Zadanie 2.6

24

24

24

24

24

24

24

Zadanie 2.7

24

24

24

24

24

24

24

Zadanie 2.8

24

24

24

24

24

Zadanie 2.9

24

24

24

24

24

24

24

Zadanie 2.10

24

24

24

24

24

Zadanie 2.11

25

25

25

25

25

25

25

25

25

25

25

25

25

25

Zadanie 2.19

26

26

26

Zadanie 2.20

26

26

26

Zadanie 2.21

26

26

26

Zadanie 2.22

26

26

26

Zadanie 2.23

26

26

26

Zadanie 2.24

26

26

26

Zadanie 2.25

27

27

27

27

27

27

27

27

27

Zadanie 2.26

27

27

27

27

27

Zadanie 2.27

27

27

27

27

27

Zadanie 2.28

27

27

27

27

27

Zadanie 2.29

27

27

27

27

Zadanie 2.31

27

27

27

Zadanie 2.32

28

28

28

Zadanie 2.33

28

28

28

28

Zadanie 2.34

28

28

28

28

28

28

28

Zadanie 2.35

28

28

28

28

Zadanie 2.36

28

28

28

28

Zadanie 2.37

28

28

28

28

Zadanie 2.38

29

29

29

Zadanie 2.39

29

29

29

Zadanie 2.40

29

29

29

Zadanie 2.41

29

29

29

Zadanie 2.42

29

29

29

Zadanie 2.43

29

29

29

Zadanie 2.44

29

29

29

29

29

Zadanie 2.45

30

30

30

30

30

Zadanie 2.46

30

30

30

30

30

30

30

Zadanie 2.47

30

30

30

30

30

30

30

Zadanie 2.48

30

30

30

30

30

30

30

Zadanie 2.49

30

30

30

30

30

30

30

Zadanie 2.50

31

31

31

31

31

31

31

Zadanie 2.51

31

31

31

31

31

31

31

Zadanie 2.52

31

31

31

31

31

31

31

Zadanie 2.53

31

31

31

31

31

31

31

Zadanie 2.54

31

31

31

31

31

31

31

Zadanie 2.55

31

31

31

31

31

31

31

Zadanie 2.56

32

32

32

32

32

Zadanie 2.57

32

32

32

32

32

Zadanie 2.58

32

32

32

Zadanie 2.59

33

33

33

33

33

33

33

33

33

33

34

34

34

34

34

34

Zadanie 11

34

34

34

34

Zadanie 13

35

35

35

35

35

Zadanie 14

35

35

35

35

35

Zadanie 15

35

35

35

35

Zadanie 16

35

35

35

Zadanie 17

35

35

35

Zadanie 18

35

35

35

35

35

35

35

36

36

36

36

36

36

36

Zadanie 26

36

36

36

36

Zadanie 27

36

36

36

36

Pełny spis treści