Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 24 - strona 36

Udowodnij, że jeśli $\text{[math]}$ i $\text{[math]}$ , to $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

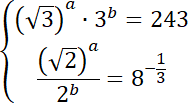
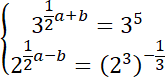
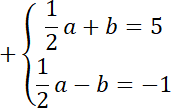
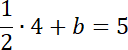
Wyznacz rozwiązanie dwóch początkowych równań. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Na tej podstawie wyznacz wartość współczynników $\text{[math]}$ i $\text{[math]}$ .

Następnie podstaw uzyskane liczby pod ostatnie równanie, skorzystaj z definicji logarytmu: $\text{[math]}$ i oblicz wynik podanego działania.

Zadanie 9, strona 13, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń. Wersja C – rozwiązania i odpowiedzi

Przykład 1, strona 255, Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 13, strona 213, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 2, strona 257, NOWA MATeMAtyka. Klasa 1. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 3.36., strona 68, Matematyka i przykłady jej zastosowań. Klasa 1. Podręcznik. Zakres podstawowy – rozwiązania i odpowiedzi

Ćwiczenie 2, strona 103, Matematyka z kluczem. Klasa 5. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 11, strona 44, Matematyka. Klasa 5. Zeszyt ćwiczeń część 1 - rozwiązania i odpowiedzi.

Zadanie 7.125., strona 206, Matematyka. Klasa 1. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 1., strona 91, Matematyka. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 19., strona 143, Matematyka. Klasa 8. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 2.1

23

23

23

23

23

23

23

23

23

Zadanie 2.2

23

23

23

23

23

23

23

23

23

Zadanie 2.3

23

23

23

23

23

23

23

Zadanie 2.4

23

23

23

23

23

23

23

Zadanie 2.5

23

23

23

23

23

23

23

Zadanie 2.6

24

24

24

24

24

24

24

Zadanie 2.7

24

24

24

24

24

24

24

Zadanie 2.8

24

24

24

24

24

Zadanie 2.9

24

24

24

24

24

24

24

Zadanie 2.10

24

24

24

24

24

Zadanie 2.11

25

25

25

25

25

25

25

25

25

25

25

25

25

25

Zadanie 2.19

26

26

26

Zadanie 2.20

26

26

26

Zadanie 2.21

26

26

26

Zadanie 2.22

26

26

26

Zadanie 2.23

26

26

26

Zadanie 2.24

26

26

26

Zadanie 2.25

27

27

27

27

27

27

27

27

27

Zadanie 2.26

27

27

27

27

27

Zadanie 2.27

27

27

27

27

27

Zadanie 2.28

27

27

27

27

27

Zadanie 2.29

27

27

27

27

Zadanie 2.31

27

27

27

Zadanie 2.32

28

28

28

Zadanie 2.33

28

28

28

28

Zadanie 2.34

28

28

28

28

28

28

28

Zadanie 2.35

28

28

28

28

Zadanie 2.36

28

28

28

28

Zadanie 2.37

28

28

28

28

Zadanie 2.38

29

29

29

Zadanie 2.39

29

29

29

Zadanie 2.40

29

29

29

Zadanie 2.41

29

29

29

Zadanie 2.42

29

29

29

Zadanie 2.43

29

29

29

Zadanie 2.44

29

29

29

29

29

Zadanie 2.45

30

30

30

30

30

Zadanie 2.46

30

30

30

30

30

30

30

Zadanie 2.47

30

30

30

30

30

30

30

Zadanie 2.48

30

30

30

30

30

30

30

Zadanie 2.49

30

30

30

30

30

30

30

Zadanie 2.50

31

31

31

31

31

31

31

Zadanie 2.51

31

31

31

31

31

31

31

Zadanie 2.52

31

31

31

31

31

31

31

Zadanie 2.53

31

31

31

31

31

31

31

Zadanie 2.54

31

31

31

31

31

31

31

Zadanie 2.55

31

31

31

31

31

31

31

Zadanie 2.56

32

32

32

32

32

Zadanie 2.57

32

32

32

32

32

Zadanie 2.58

32

32

32

Zadanie 2.59

33

33

33

33

33

33

33

33

33

33

34

34

34

34

34

34

Zadanie 11

34

34

34

34

Zadanie 13

35

35

35

35

35

Zadanie 14

35

35

35

35

35

Zadanie 15

35

35

35

35

Zadanie 16

35

35

35

Zadanie 17

35

35

35

Zadanie 18

35

35

35

35

35

35

35

36

36

36

36

36

36

36

Zadanie 26

36

36

36

36

Zadanie 27

36

36

36

36

Pełny spis treści