Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 27, b) - strona 36

Oblicz wyraz ogólny ciągu $\text{[math]}$ w przypadku, gdy ten ciąg nie jest monotoniczny, jeśli liczby $\text{[math]}$ , są w podanej kolejności trzema początkowymi wyrazami nieskończonego ciągu geometrycznego $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

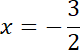
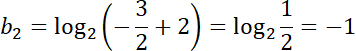
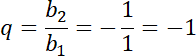
Na podstawie podpunktu a) znasz wartość $\text{[math]}$ . Zauważ, że ciąg nie jest monotoniczny, gdy jego wyrazy są raz ujemne, a raz dodatnie. Podstaw go pod podane liczby i wyznacz dokładne wartości trzech początkowych wyrazów ciągu geometrycznego.

Następnie oblicz iloraz ciągu $\text{[math]}$ , korzystając z tego, że jest ona równa ilorazowi dwóch sąsiednich wyrazów i wyznacz jego wzór ogólny korzystając ze wzoru: $\text{[math]}$ .

Zadanie 4., strona 77, Matematyka wokół nas. Klasa 5. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 12., strona 84, Matematyka. Klasa 5. Podręcznik. Część 2 – rozwiązania i odpowiedzi

Zadanie 30., strona 37, Matematyka. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 138., strona 140, Matematyka z plusem. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 14, strona 212, Matematyka. Klasa 4. Podręcznik - rozwiązania i odpowiedzi

Zadanie 22, strona 78, Matematyka z kluczem. Klasa 4. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 16, strona 173, Matematyka z kluczem. Klasa 4. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 19., strona 273, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 7., strona 25, Matematyka wokół nas. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie 4., strona 30, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń - pytania i odpowiedzi.

Zadanie 2.1

23

23

23

23

23

23

23

23

23

Zadanie 2.2

23

23

23

23

23

23

23

23

23

Zadanie 2.3

23

23

23

23

23

23

23

Zadanie 2.4

23

23

23

23

23

23

23

Zadanie 2.5

23

23

23

23

23

23

23

Zadanie 2.6

24

24

24

24

24

24

24

Zadanie 2.7

24

24

24

24

24

24

24

Zadanie 2.8

24

24

24

24

24

Zadanie 2.9

24

24

24

24

24

24

24

Zadanie 2.10

24

24

24

24

24

Zadanie 2.11

25

25

25

25

25

25

25

25

25

25

25

25

25

25

Zadanie 2.19

26

26

26

Zadanie 2.20

26

26

26

Zadanie 2.21

26

26

26

Zadanie 2.22

26

26

26

Zadanie 2.23

26

26

26

Zadanie 2.24

26

26

26

Zadanie 2.25

27

27

27

27

27

27

27

27

27

Zadanie 2.26

27

27

27

27

27

Zadanie 2.27

27

27

27

27

27

Zadanie 2.28

27

27

27

27

27

Zadanie 2.29

27

27

27

27

Zadanie 2.31

27

27

27

Zadanie 2.32

28

28

28

Zadanie 2.33

28

28

28

28

Zadanie 2.34

28

28

28

28

28

28

28

Zadanie 2.35

28

28

28

28

Zadanie 2.36

28

28

28

28

Zadanie 2.37

28

28

28

28

Zadanie 2.38

29

29

29

Zadanie 2.39

29

29

29

Zadanie 2.40

29

29

29

Zadanie 2.41

29

29

29

Zadanie 2.42

29

29

29

Zadanie 2.43

29

29

29

Zadanie 2.44

29

29

29

29

29

Zadanie 2.45

30

30

30

30

30

Zadanie 2.46

30

30

30

30

30

30

30

Zadanie 2.47

30

30

30

30

30

30

30

Zadanie 2.48

30

30

30

30

30

30

30

Zadanie 2.49

30

30

30

30

30

30

30

Zadanie 2.50

31

31

31

31

31

31

31

Zadanie 2.51

31

31

31

31

31

31

31

Zadanie 2.52

31

31

31

31

31

31

31

Zadanie 2.53

31

31

31

31

31

31

31

Zadanie 2.54

31

31

31

31

31

31

31

Zadanie 2.55

31

31

31

31

31

31

31

Zadanie 2.56

32

32

32

32

32

Zadanie 2.57

32

32

32

32

32

Zadanie 2.58

32

32

32

Zadanie 2.59

33

33

33

33

33

33

33

33

33

33

34

34

34

34

34

34

Zadanie 11

34

34

34

34

Zadanie 13

35

35

35

35

35

Zadanie 14

35

35

35

35

35

Zadanie 15

35

35

35

35

Zadanie 16

35

35

35

Zadanie 17

35

35

35

Zadanie 18

35

35

35

35

35

35

35

36

36

36

36

36

36

36

Zadanie 26

36

36

36

36

Zadanie 27

36

36

36

36

Pełny spis treści