Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Podręcznik, Wydawnictwo: OE Pazdro

Zadanie 2.39, b) - strona 29

Narysuj wykres funkcji $\text{[math]}$ , podaj jej dziedzinę i ustal rachunkowo, czy do wykresu funkcji $\text{[math]}$ należy punkt $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Punkt A należy do wykresu funkcji $\text{[math]}$ .

Skorzystaj z tego, że dla logarytmu $\text{[math]}$ liczba logarytmowana $\text{[math]}$ musi być większa od 0. Zapisz to za pomocą nierówności i wyznacz z niej wartość $\text{[math]}$ .

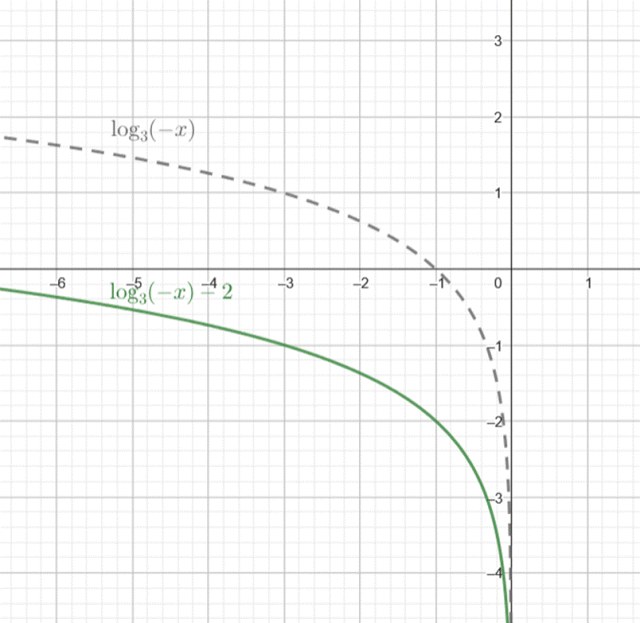
Na podstawie wykresu funkcji $\text{[math]}$ , gdzie $\text{[math]}$ jest wektorem przesunięcia wykresu funkcji $\text{[math]}$ , naszkicuj wykres podanej funkcji przesuwając wyjściowy wykres logarytmu o $\text{[math]}$ jednostek wzdłuż osi OX i $\text{[math]}$ jednostek wzdłuż osi OY.

Następnie sprawdź, czy podany punkt należy do wykresu funkcji, czyli wstaw w miejsce $\text{[math]}$ pierwszą współrzędną punktu A i sprawdź, czy wynik będzie równy jego drugiej współrzędnej.

Zadanie 12, strona 22, Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2023

Zadanie 8, strona 173, Matematyka. Klasa 2. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zadanie 23, strona 80, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 2.19, strona 20, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 19., strona 119, Matematyka. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie 9, strona 186, MATeMAtyka. Klasa 1. Zbiór zadań. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie 7, strona 53, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 5, strona 39, Matematyka z kluczem. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 3., strona 33, Matematyka. Klasa 3. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 15, strona 39, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Zadanie 2.1

23

23

23

23

23

23

23

23

23

Zadanie 2.2

23

23

23

23

23

23

23

23

23

Zadanie 2.3

23

23

23

23

23

23

23

Zadanie 2.4

23

23

23

23

23

23

23

Zadanie 2.5

23

23

23

23

23

23

23

Zadanie 2.6

24

24

24

24

24

24

24

Zadanie 2.7

24

24

24

24

24

24

24

Zadanie 2.8

24

24

24

24

24

Zadanie 2.9

24

24

24

24

24

24

24

Zadanie 2.10

24

24

24

24

24

Zadanie 2.11

25

25

25

25

25

25

25

25

25

25

25

25

25

25

Zadanie 2.19

26

26

26

Zadanie 2.20

26

26

26

Zadanie 2.21

26

26

26

Zadanie 2.22

26

26

26

Zadanie 2.23

26

26

26

Zadanie 2.24

26

26

26

Zadanie 2.25

27

27

27

27

27

27

27

27

27

Zadanie 2.26

27

27

27

27

27

Zadanie 2.27

27

27

27

27

27

Zadanie 2.28

27

27

27

27

27

Zadanie 2.29

27

27

27

27

Zadanie 2.31

27

27

27

Zadanie 2.32

28

28

28

Zadanie 2.33

28

28

28

28

Zadanie 2.34

28

28

28

28

28

28

28

Zadanie 2.35

28

28

28

28

Zadanie 2.36

28

28

28

28

Zadanie 2.37

28

28

28

28

Zadanie 2.38

29

29

29

Zadanie 2.39

29

29

29

Zadanie 2.40

29

29

29

Zadanie 2.41

29

29

29

Zadanie 2.42

29

29

29

Zadanie 2.43

29

29

29

Zadanie 2.44

29

29

29

29

29

Zadanie 2.45

30

30

30

30

30

Zadanie 2.46

30

30

30

30

30

30

30

Zadanie 2.47

30

30

30

30

30

30

30

Zadanie 2.48

30

30

30

30

30

30

30

Zadanie 2.49

30

30

30

30

30

30

30

Zadanie 2.50

31

31

31

31

31

31

31

Zadanie 2.51

31

31

31

31

31

31

31

Zadanie 2.52

31

31

31

31

31

31

31

Zadanie 2.53

31

31

31

31

31

31

31

Zadanie 2.54

31

31

31

31

31

31

31

Zadanie 2.55

31

31

31

31

31

31

31

Zadanie 2.56

32

32

32

32

32

Zadanie 2.57

32

32

32

32

32

Zadanie 2.58

32

32

32

Zadanie 2.59

33

33

33

33

33

33

33

33

33

33

34

34

34

34

34

34

Zadanie 11

34

34

34

34

Zadanie 13

35

35

35

35

35

Zadanie 14

35

35

35

35

35

Zadanie 15

35

35

35

35

Zadanie 16

35

35

35

Zadanie 17

35

35

35

Zadanie 18

35

35

35

35

35

35

35

36

36

36

36

36

36

36

Zadanie 26

36

36

36

36

Zadanie 27

36

36

36

36

Pełny spis treści