![]()
![]()
![]()
![]()
![]()
![]()
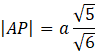
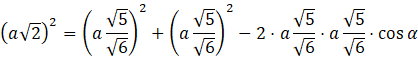
![]()
![]()
![]()
![]()
![]()
ODP.:
![]()

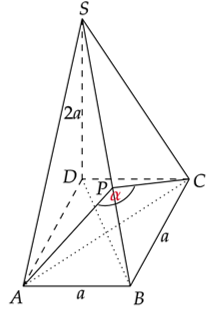
Wykonaj rysunek pomocniczy.
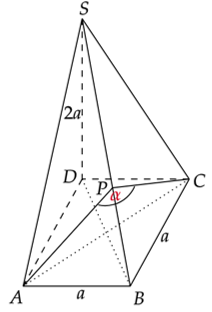
Zauważ, że trójkąt SAB i SCB jest prostokątny. Bok AB jest prostopadły do boku AD i DS. Co za tym idzie do ściany bocznej ADS. Więc bok AD jest prostopadły do krawędzi AS. Analogicznie dla boku BC.
Skorzystaj z twierdzenia Pitagorasa w trójkącie ADS.
![]()
![]()
![]()
![]()
![]()
Zauważ, że trójkąty ADS i SDC są podobne z cechy bok, kąt, bok (
![]() .
.
![]()
Oblicz długość przekątnej podstawy, czyli kwadratu.
![]()
Skorzystaj z twierdzenia Pitagorasa w trójkącie SBD.
![]()
![]()
![]()
![]()
![]()
Zauważ, że odcinek AP jest wysokością trójkąt ASB. Skorzystaj ze wzoru na pole trójkąta.
![]()
![]()
Z powstałego równania wylicz długość boku AP.
![]()
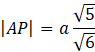
Skorzystaj z twierdzenia cosinusów w trójkącie APC i oblicz wartość cosinusa.
![]()
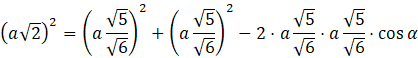
![]()
![]()
![]()
![]()
Skorzystaj z jedynki trygonometrycznej i oblicz wartość sinusa.
![]()
![]()
![]()
![]()
![]()
Zauważ, że sinus nie może być ujemny, ponieważ wtedy miałby miarę większą od
![]() . Co jest niemożliwe w tym przypadku.
. Co jest niemożliwe w tym przypadku.
![]()