Oblicz dla jakiego m funkcja
ma dwa pierwiastki spełniające warunek
.
– sprzeczne z treścią zadania
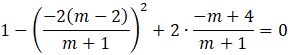
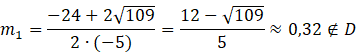
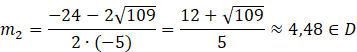
ODP.:
Równanie ma dwa rozwiązania wtedy gdy delta jest większa od zera. Oblicz dla jakich m:
.
Oblicz dla jakiego m każdy z nawiasów się zeruje.
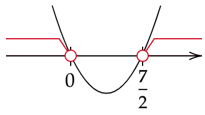
Zapisz powyższe rozwiązania na osi. Ramiona paraboli skieruj do góry. Zaznacz dla jakich x parabola jest nad osią.
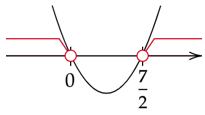
Zapisz zaznaczony przedział nierówności.
Zastosuj wzory Viete’a do powyższego równania.
Przekształć równanie
do otrzymania postaci ze wzorami Viete’a. Skorzystaj ze wzoru skróconego mnożenia na różnicę kwadratów.
Przenieś wszystko na lewą stronę równania.
Wyłącz wspólny czynnik przed nawias.
Zauważ, że powstały trzy nawiasy. Sprawdź dla jakich m każdy z nich wyzeruję się.
Oblicz pierwszy z nawiasów.
– sprzeczne z treścią zadania, ponieważ pierwiastki trójmianu są różne.
Oblicz drugi z nawiasów.
Skorzystaj z wyliczonych wzorów Viete’a.
Oblicz trzeci z nawiasów. Doprowadź równanie do otrzymania postaci ze wzorami Viete’a.
Podstaw wyliczone wzory Viete’a.
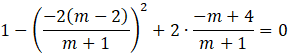
Zauważ, że powstało równanie kwadratowe. Oblicz deltę i miejsca zerowe.
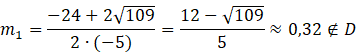
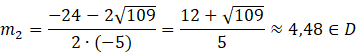
Zauważ, że jedynym rozwiązaniem spełniającym warunki zadania jest
.