Zadanie
W tym zadaniu oblicz, ile razy większa jest objętość sześcianu, którego każdą krawędź zwiększono o 100%, jeśli początkowo jego krawędź miała długość 2,5 cm.
Rozwiązanie
Długość zwiększonej krawędzi:
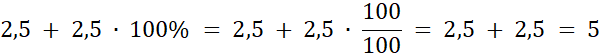
Początkowa objętość sześcianu: (2,5)3 = 2,5 ∙ 2,5 ∙ 2,5 = 15,625 cm3
Objętość zwiększonego sześcianu: 53 = 5 ∙ 5 ∙ 5 = 125 cm3
Iloraz objętości: 125 : 15,625 = 125000 : 15625 = 8
Sześcian o przedłużonych krawędziach jest 8 razy większy.
Wyjaśnienie
Procent to ułamek, który w liczniku ma liczbę procent, a w mianowniku liczbę 100. Objętość sześcianu jest równa długości jego krawędzi podniesionej do potęgi 3. Żeby sprawdzić, ile razy większy sześcian dzielimy większą objętość przez mniejszą.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
Figury przestrzenne
140
Graniastosłupy proste. Pole powierzchni graniastosłupa
140
Zadanie 1 zamknięte
140Zadanie 2 zamknięte
140Zadanie 8 zamknięte
142Zadanie 1.
143Zadanie 6.
144Zadanie 9.
144Zadanie 10.
145
Objętość prostopadłościanu
145
Zadanie 7 zamknięte
146Zadanie 17 zamknięte
147Zadanie 1.
148Zadanie 7.
149Zadanie 12.
149Zadanie 13.
150Zadanie 14.
150Zadanie 19.
150Zadanie 21.
151
Ostrosłupy
151
Zadanie 6 zamknięte
153Zadanie 11 zamknięte
154
Bryły obrotowe
156
Zadanie 2 zamknięte
156Zadanie 4 zamknięte
157Zadanie 6 zamknięte
157Zadanie 10 zamknięte
159Zadanie 4.
160Zadanie 7.
161Zadanie 10.
161