Musisz ustalić dla jakich wartości suma zadanych wielomianów jest wielomianem konkretnego stopnia.
Zadany wielomian jest:
· wielomianem pierwszego stopnia dla: a = -4 i b=4
· wielomianem drugiego stopnia dla: a=2-b i b≠1
· wielomianem trzeciego stopnia dla: a≠2-b i b∈R

![]()
![]()
![]()
Otrzymany wielomian będzie:
· Wielomianem zerowego stopnia, gdy:
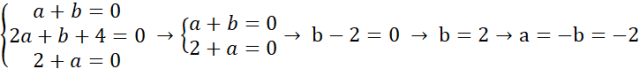
Sprawdźmy na pozostałym równaniu:
![]()
· Wielomianem pierwszego stopnia, gdy:
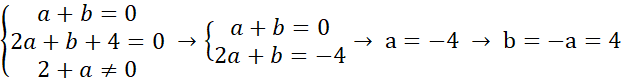
Sprawdźmy na pozostałej nierówności:
![]()
· Wielomianem drugiego stopnia, gdy:
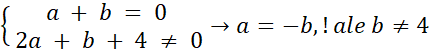
· Wielomianem trzeciego stopnia, gdy:
![]()

Zadanie 1.2.
65Zadanie 1.3.
65Zadanie 1.4.
66Zadanie 1.5.
66Zadanie 1.6.
66Zadanie 1.7.
66Zadanie 1.8.
66Zadanie 1.9.
67Zadanie 1.10.
67Zadanie 1.11.
67Zadanie 1.12.
67Zadanie 1.13.
67Zadanie 2.4.
72Zadanie 2.5.
72Zadanie 2.6.
72Zadanie 2.7.
72Zadanie 2.8.
73Zadanie 2.9.
73Zadanie 2.12.
73Zadanie 2.18.
74Zadanie 3.2.
76Zadanie 3.3.
76Zadanie 3.4.
77Zadanie 3.5.
77Zadanie 3.6.
77Zadanie 3.7.
77Zadanie 3.10.
77Zadanie 3.14.
78Zadanie 4.1.
86Zadanie 4.2.
86Zadanie 4.3.
87Zadanie 4.5.
87Zadanie 4.6.
87Zadanie 4.10.
87Zadanie 4.11.
87Zadanie 4.12.
87Zadanie 4.13.
88Zadanie 4.15.
88Zadanie 4.16.
88Zadanie 4.17.
88Zadanie 4.18.
89Zadanie 4.19.
89Zadanie 4.20.
89Zadanie 4.21.
89Zadanie 5.2.
96Zadanie 5.3.
96Zadanie 5.5.
96Zadanie 5.12.
97Zadanie 5.13.
97Zadanie 5.14.
97Zadanie 5.15.
97Zadanie 6.2.
106Zadanie 6.3.
106Zadanie 6.6.
107Zadanie 6.7.
107Zadanie 6.8.
107Zadanie 6.9.
107Zadanie 6.10.
107Zadanie 6.11.
107Zadanie 7.3.
114Zadanie 7.4.
114Zadanie 7.5.
114Zadanie 7.6.
114Zadanie 7.7.
115Zadanie 7.8.
115Zadanie 7.9.
115Zadanie 7.17.
116Zadanie 7.18.
116Zadanie 7.19.
116Zadanie 8.2.
124Zadanie 8.3.
124Zadanie 8.4.
124Zadanie 8.5.
124Zadanie 8.6.
125Zadanie 8.7.
125Zadanie 8.8.
125Zadanie 8.9.
125Zadanie 8.10.
125Zadanie 8.11.
125Zadanie 8.12.
126Zadanie 9.3.
131Zadanie 9.4.
131Zadanie 9.5.
131Zadanie 9.6.
131Zadanie 9.7.
132Zadanie 28.
136Zadanie 29.
137Zadanie 32.
137Zadanie 33.
137Zadanie 34.
137Zadanie 46.
138Zadanie 47.
138
