Musisz przekształcić podany wielomian w taki sposób, by udowodnić zadaną zależność.
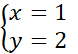

![]()
![]()
![]()
Niech:
![]()
![]()
Szukane liczby x i y muszą być naturalne oraz dodatnie, więc również ich suma k jest naturalna i dodatnia. Iloczyn sumy k oraz sumy pomniejszonej o dwa k-2 wynosi 8, więc obie te liczby muszą być dzielnikami liczby 8.
Wypiszmy dodatnie dzielniki liczby 8 w parach:
![]()
Możemy zauważyć, że jedyną parą dzielników pasujących do założenia (*) są liczby 2 i 4, więc:
![]()
Jedyną parą dodatnich liczb naturalnych spełniającą założenie (**) jest:

Zadanie 1.2.
65Zadanie 1.3.
65Zadanie 1.4.
66Zadanie 1.5.
66Zadanie 1.6.
66Zadanie 1.7.
66Zadanie 1.8.
66Zadanie 1.9.
67Zadanie 1.10.
67Zadanie 1.11.
67Zadanie 1.12.
67Zadanie 1.13.
67Zadanie 2.4.
72Zadanie 2.5.
72Zadanie 2.6.
72Zadanie 2.7.
72Zadanie 2.8.
73Zadanie 2.9.
73Zadanie 2.12.
73Zadanie 2.18.
74Zadanie 3.2.
76Zadanie 3.3.
76Zadanie 3.4.
77Zadanie 3.5.
77Zadanie 3.6.
77Zadanie 3.7.
77Zadanie 3.10.
77Zadanie 3.14.
78Zadanie 4.1.
86Zadanie 4.2.
86Zadanie 4.3.
87Zadanie 4.5.
87Zadanie 4.6.
87Zadanie 4.10.
87Zadanie 4.11.
87Zadanie 4.12.
87Zadanie 4.13.
88Zadanie 4.15.
88Zadanie 4.16.
88Zadanie 4.17.
88Zadanie 4.18.
89Zadanie 4.19.
89Zadanie 4.20.
89Zadanie 4.21.
89Zadanie 5.2.
96Zadanie 5.3.
96Zadanie 5.5.
96Zadanie 5.12.
97Zadanie 5.13.
97Zadanie 5.14.
97Zadanie 5.15.
97Zadanie 6.2.
106Zadanie 6.3.
106Zadanie 6.6.
107Zadanie 6.7.
107Zadanie 6.8.
107Zadanie 6.9.
107Zadanie 6.10.
107Zadanie 6.11.
107Zadanie 7.3.
114Zadanie 7.4.
114Zadanie 7.5.
114Zadanie 7.6.
114Zadanie 7.7.
115Zadanie 7.8.
115Zadanie 7.9.
115Zadanie 7.17.
116Zadanie 7.18.
116Zadanie 7.19.
116Zadanie 8.2.
124Zadanie 8.3.
124Zadanie 8.4.
124Zadanie 8.5.
124Zadanie 8.6.
125Zadanie 8.7.
125Zadanie 8.8.
125Zadanie 8.9.
125Zadanie 8.10.
125Zadanie 8.11.
125Zadanie 8.12.
126Zadanie 9.3.
131Zadanie 9.4.
131Zadanie 9.5.
131Zadanie 9.6.
131Zadanie 9.7.
132Zadanie 28.
136Zadanie 29.
137Zadanie 32.
137Zadanie 33.
137Zadanie 34.
137Zadanie 46.
138Zadanie 47.
138
