W tym zadaniu musisz obliczyć wysokość trójkąta prostokątnego, która jest poprowadzona z przyprostokątnej na przeciwprostokątną trójkąta prostokątnego.
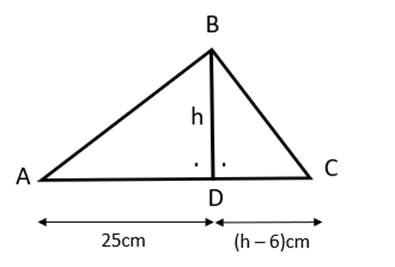
h–wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną [cm]
h > 0 i h–6 > 0⇒ h > 6
Z podobieństwa trójkątów: BDC i ADB:
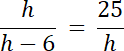
h2 = 25(h–6)
h2 = 25h–150 |–25h + 150
h2–25h + 150 = 0
∆ = (–25)2–4∙150∙1
∆ = 625–600
∆ = 25 | √
√∆ = 5
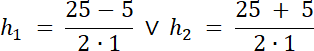
![]() , gdzie
, gdzie
![]() , więc:
, więc:
h = 10 cm ∨ h = 15 cm

Na początku narysuj rysunek pomocniczy, aby zauważyć pewne zależności: po opuszczeniu wysokości na przeciwprostokątną w trójkącie prostokątnym powstały dwa trójkąty prostokątne–korzystasz tu z własności podobieństwa trójkątów:
![]() i na podstawie tego równania wyznaczasz wysokość trójkąta prostokątnego przy odpowiednich założeniach.
i na podstawie tego równania wyznaczasz wysokość trójkąta prostokątnego przy odpowiednich założeniach.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
