W tym zadaniu należy narysować wykres paraboli funkcji kwadratowej i omówić własności tej funkcji.
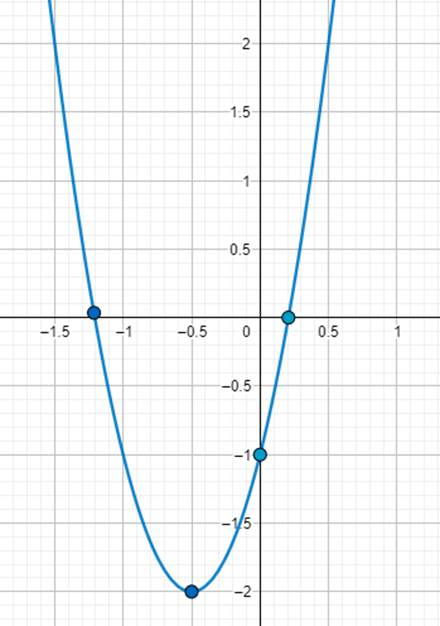
–dziedzina funkcji (D): x ⋲ R
–zbiór wartości (Zw) y ⋲ <–2, + ∞)
–f(x) > 0
–f(x) < 0
–funkcja przecina oś OY w punkcie (0,–1)
–funkcja nie przyjmuje wartości największej
–oś symetrii funkcji: x = –0,5
–funkcja jest rosnąca w przedziale x ⋲ <–0,5, + ∞), a maleje w przedziale x ⋲ (–∞, 0,5>
–funkcja ma dwa miejsca zerowe, ponieważ wykres paraboli przecina oś OX w dwóch punktach
–funkcja osiąga wartość minimalną w punkcie, gdzie znajduje się wierzchołek narysowanej funkcji, ponieważ współczynnik kierunkowy a > 0
–miejsca zerowe funkcji f: f(x) = 0 ⇔ 4x2 + 4x–1
4x2 + 4x–1 = 0
∆ = b2–4ac
∆ = 16 + 16
∆ = 32
![]()
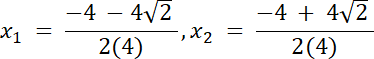
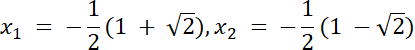
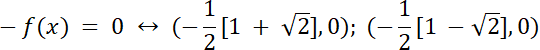

Własności funkcji odczytujemy z wykresu na tyle, na ile jest to możliwe. Zbiór wartości funkcji wyznacz na podstawie pierwszej współrzędnej wierzchołka paraboli, którą odczytujemy z wykresu i wstawiamy do wzoru funkcji.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
