W tym zadaniu należy wyznaczyć wzór funkcji kwadratowej w postaci kanonicznej na podstawie danych z treści zadania.
f(x) = a(x–p)2 + q
f(–2) = f(10) = 0
x1 = –2, x2 = 10
Wierzchołek funkcji f: W(p, q)
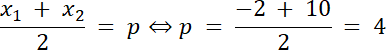
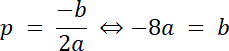
f(x) = ax2 + bx + c, f(0) = –5 ⇔ c = –5
f(x) = ax2–8ax–5
a(–2)2–8a(–2)–5 = 0
4a + 16a = 5 ⇔ 20a = 5 | /20
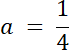
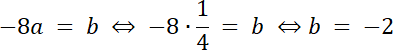
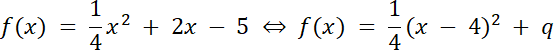
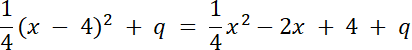
4 + q = –5 |–4
q = –9
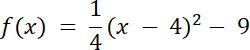

Punkty o argumentach–2 i 10 są oddalone o taką sama odległość od wierzchołka paraboli funkcji kwadratowej, więc argument wierzchołka wyznacz ze wzoru na środek odcinka. Następnie korzystamy ze wzoru na wyznaczenie wartości x dla wierzchołka paraboli i wyznacz zależność dla współczynników a i b. Najpierw zapisz wzór w postaci ogólnej i obliczmy wartość liczby c, a następnie przyrównaj wzory funkcji f w postaci kanonicznej i w postaci ogólnej, co pozwoli nam na wyznaczenie wartości q. Na koniec zapisz wzór funkcji w postaci kanonicznej.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
