W tym zadaniu należy zapisać wzór funkcji kwadratowej, który opisze pole powierzchni nowego prostokąta, w zależności od długości boków x. Należy określić dziedzinę dla tej funkcji i wyznaczyć pole prostokąta, który będzie miał największą powierzchnię.
Wymiary nowego prostokąta:
10 + x⇒ jeden z boków prostokąta [cm]
16–x⇒ drugi bok prostokąta [cm]
Dziedzina:
x > 0 ∧10 + x > 0 ⇒ x >–10 ∧16–x > 0 ⇒ x < 16
x ⋲ (0, 16)
f(x) = (10 + x)(16–x), gdzie x ⋲ (0, 16)
f(x) = –x2 + 6x + 160
a < 0, więc ymax = f(p), gdzie p to argument wierzchołka funkcji
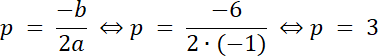
10 + x = 10 + 3 = 13 cm–jeden z boków prostokąta [cm]
16–x = 16–3 = 13 cm–drugi bok prostokąta [cm]
f(3) = 13⋅13 ⇔ f(3) = 169 cm2

Współczynnik a funkcji f jest mniejszy od zera, więc funkcja f osiąga wartość maksymalną w wierzchołku paraboli. Wyznacz argument wierzchołka, a następnie wyznacz pole największego prostokąta.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
