W tym zadaniu należy wyznaczyć wzór funkcji kwadratowej w postaci ogólnej na podstawie danych z treści zadania.
x = 4–argument wierzchołka funkcji kwadratowej f
f(6) = 0 ⇔ x ⋲ {6, x2}
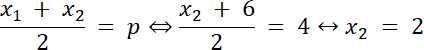
f(x) = a(x–2)(x–6)
Należy rozważyć dwa przypadki:
1) Ramiona paraboli są skierowane do góry, wierzchołek funkcji osiąga wartość minimalną, więc f(3) = –2
f(3) = a(3–2)(3–6)
f(3) = a∙1∙(–3)
–3a = –2 | /(–3)
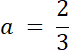
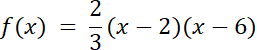
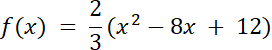
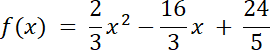
2) Ramiona paraboli są skierowane do góry, wierzchołek funkcji osiąga wartość maksymalną, więc f(1) = –2
f(1) = a(1–2)(1–6)
f(1) = a(–1)(–5)
–5a = 2 | /(–5)
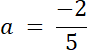
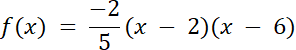
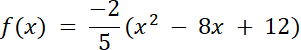
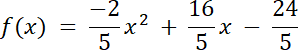

Argument wierzchołka określamy na podstawie osi symetrii wykresu funkcji f. Drugie miejsce zerowe wyznacz ze średniej arytmetycznej miejsc zerowych, które dają wartość argumentu wierzchołka. Następnie zauważmy, że ramiona funkcji mogą być albo skierowanie ku górze, albo ku dołowi, wiec na tej postawie rozważamy 2 przypadki, aby wyznaczyć wzór funkcji kwadratowej f.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
