W tym zadaniu należy wyznaczyć wzór funkcji kwadratowej w postaci ogólnej na podstawie danych z treści zadania.
Wierzchołek funkcji w(p, q), gdzie p = –3
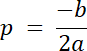
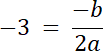
![]()
f(x) = ax2 + bx + c
f(0) = 1 ⇔ c = 1, a < 0
f(x) = ax2 + 6ax + 1
f(–9) = –8
f(–9) = a∙(–9)2 + 6a∙(–9) + 1
81a–54a + 1 = –8 |–1
27a = –9 | /27
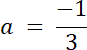
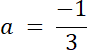
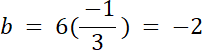
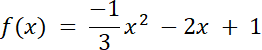

Funkcja kwadratowa zmienia swój przedział monotoniczności dla wierzchołka paraboli, więc argument x = –3. Dodatkowo możemy stwierdzić, że wartość maksymalną funkcja osiąga w wierzchołku funkcji, ponieważ od lewej strony od wierzchołka parabola ma coraz mniejsze wartości y. Punkt z argumentem x = 9 znajduje się dalej w układzie współrzędnych niż punkt dla x = –4, patrząc na odległość od wierzchołka funkcji. Ze wzoru na współrzędną x wierzchołka wyznacz zależność między współczynnikami a i b, a współczynnik c oblicz, wstawiając do wzoru funkcji f punkt (0,1). Na koniec zapisz wzór funkcji kwadratowej w postaci ogólnej.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
