W tym zadaniu musisz sprawdzić, czy dane równanie ma więcej niż jedno rozwiązanie (wskazane w treści zadania). Jeśli tak jest, to oblicz je.
x2–(a2 + 2)x + 4a + 1 = 0 dla x = 3
(3)2–(a2 + 2)∙3 + 4a + 1 = 0
9–(3a2 + 6) + 4a + 1 = 0
10–3a2–6 + 4a = 0
–3a2 + 4a + 4 = 0
∆ = (4)2–4∙(–3)∙4
∆ = 16 + 48
∆ = 64 | /√
√∆ = 8
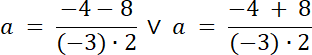
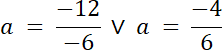
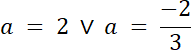
Dwa przypadki:
1. x2–(a2 + 2)x + 4a + 1 = 0 dla a = 2
x2–(22 + 2)x + 4∙2 + 1 = 0
x2–6x + 9 = 0
(x–3)2 = 0
Dla a = 2 równanie posiada tylko jedno rozwiązanie.
2.
![]() dla
dla
![]()
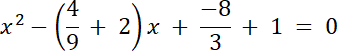
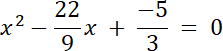
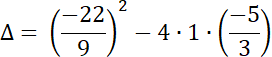
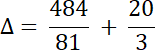
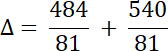
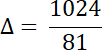
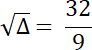
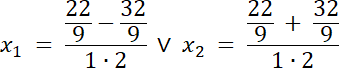
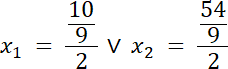
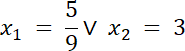

Na podstawie podanego rozwiązania równania, wyznacz wartość współczynnika a, a następnie oblicz czy istnieją inne rozwiązania tego równania.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
