W tym zadaniu trzeba rozwiązać równanie dwukwadratowe, wprowadzając do niego pomocniczą zmienną, aby doprowadzić je do równania kwadratowego i obliczyć rozwiązania równania.
3(2x2 + 5x)2 + 6(2x2 + 5x) = 0
t = 2x2 + 5x
3t2 + 6t = 0
3t(t + 2) = 0
t = 0 ∨ t = –2,
2x2 + 5x = 0 ∨ 2x2 + 5x = –2
x(2x + 5) = 0 ∨ 2x2 + 5x + 2 = 0
x = 0 ∨ 2x + 5 = 0 ∨ 2x + 5x + 2 = 0
x = 0 ∨ 2x = –5 ∨ 2x + 5x + 2 = 0
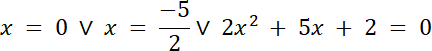
dla 2x + 5x + 2 = 0:
∆ = (5)2–4∙2∙2
∆ = 25–16
∆ = 9 | √
√∆ = 3
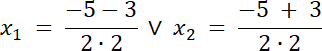
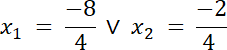
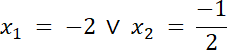
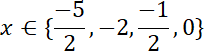

Na początku musisz wprowadzić pomocniczą zmienną t, gdzie: t = 2x2 + 5x, a następnie obliczyć wartość liczby t. W kolejnym kroku, w celu wyznaczenia wszystkich rozwiązań równania, należy rozwiązać równanie kwadratowe: 2x + 5x + 2 = 0. Po wykorzystaniu wzoru na wyznacznik oraz wyznaczeniu rozwiązań równania podajemy pełny zbiór rozwiązań liczby x.

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
