W tym zadaniu należy udowodnić, że funkcja f dla x ⋲<–4√2,–3√2> ma największą wartość dla f(–3√2), a najmniejsza wynosi f(–4√2).
f(x) = –12 ⇔ x ⋲ {–6, 2}
x1 = –6 i x2 = 2
wierzchołek funkcji W(p, q)
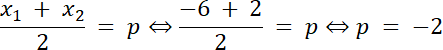
f(0) > f(2) i f(0) > f(–6), więc ymax = f(–2)
funkcja f jest rosnąca w przedziale: x ⋲ (–∞,–2>, a malejąca x ⋲ (–2, + ∞)
–4√2 <–3√2 <–2, więc f(–4√2) < f(–3√2) < f(–2), czyli powyższe założenie jest prawdziwe.

Należy wyznaczyć wartość argumentu wierzchołka funkcji kwadratowej. Zauważmy, że wierzchołek znajduje się w punkcie x = –2. Dodatkowo zauważmy, że f(0) > f(2) i f(0) > f(–6), czyli funkcja ma ramiona skierowane ku dołowi, co oznacza, że wartość maksymalną funkcja osiąga dla wierzchołka paraboli. Skoro wiemy, że w przedziale (–∞,–2> funkcja jest rosnąca, argument, który znajduje się bliżej wierzchołka paraboli, osiąga większą wartość, więc funkcja f dla x ⋲<–4√2,–3√2> ma największą wartość dla f(–3√2), a najmniejszą dla f(–4√2).

Ćwiczenie 1.
56Ćwiczenie 2.
57Ćwiczenie 4.
58Zadanie 1.
59Zadanie 2.
59Zadanie 3.
59Zadanie 4.
59Zadanie 5.
59Zadanie 6.
59Zadanie 7.
60Zadanie 8.
60Zadanie 9.
60Zadanie 1.
64Zadanie 2.
64Zadanie 3.
64Zadanie 4.
64Zadanie 5.
64Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Ćwiczenie 1.
65Ćwiczenie 3.
69Zadanie 1.
71Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 5.
71Zadanie 6.
71Zadanie 7.
71Zadanie 8.
71Zadanie 9.
71Zadanie 10.
71Ćwiczenie 1.
72Zadanie 1.
74Zadanie 2.
74Zadanie 3.
74Zadanie 4.
74Zadanie 1.
81Zadanie 2.
81Zadanie 3.
82Zadanie 5.
82Ćwiczenie 1.
85Zadanie 4.
87Zadanie 8.
87Zadanie 1.
90Zadanie 2.
90Zadanie 3.
90Zadanie 4.
90Zadanie 5.
90Zadanie 6.
90Zadanie 7.
90Zadanie 8.
91Zadanie 9.
91Zadanie 10.
91Zadanie 11.
91Zadanie 12.
91Zadanie 13.
91Zadanie 17.
91Ćwiczenie 1.
92Zadanie 1.
92Zadanie 2.
92Zadanie 3.
93Zadanie 4.
93Zadanie 5.
93Ćwiczenie 1.
96Ćwiczenie 2.
96Zadanie 1.
96Zadanie 2.
97Zadanie 3.
97Zadanie 4.
97Zadanie 5.
97Zadanie 6.
97Zadanie 7.
97Zadanie 8.
97Zadanie 9.
97Zadanie 12.
103Zadanie 13.
103Zadanie 14.
103Zadanie 17.
103Zadanie 18.
103Zadanie 19.
103Zadanie 21.
103
