Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2023

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 7 - strona 12

Wyznacz wartość zmiennej $\text{[math]}$ $\text{[math]}$ dla którego suma nieskończonego szeregu geometrycznego $\text{[math]}$ istnieje i jest równa $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

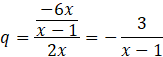
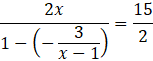
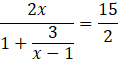
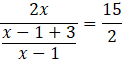
ODP: Suma szeregu geometrycznego jest równa $\text{[math]}$ dla $\text{[math]}$ .

$\text{[math]}$

Na podstawie powyższego wzoru zapisz pierwszy wyraz ciągu.

$\text{[math]}$

Podziel wartość drugiego wyrazu ciągu przez wartość pierwszego. W ten sposób wyznasz iloraz ciągu.

$\text{[math]}$

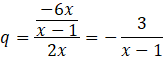
Zauważ, że aby szereg istniał, to $\text{[math]}$ .

$\text{[math]}$

Skorzystaj z tego, że wartość bezwzględną ilorazu możesz zamienić na iloraz wartości bezwzględnych. Pomnóż całą nierówność przez mianownik ułamka znajdującego się z lewej strony nierówności.

$\text{[math]}$

Skorzystaj z tego, że nierówność typu $\text{[math]}$ zapisuję się jako dwie nierówności: $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zapisz przedział do którego należy $\text{[math]}$ . Uwzględnij powyższe nierówności i warunki podane w treści zadania.

$\text{[math]}$

Wyznaczyłeś $\text{[math]}$ dla których $\text{[math]}$ , możesz więc skorzystać ze wzoru na sumę wyrazów nieskończonego ciągu geometrycznego.

$\text{[math]}$

Pod powyższe równanie podstaw znane wartości i wyznacz wartość $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

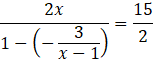
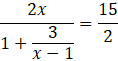
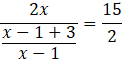
Pomnóż na skos i przenieś wszystkie wartości na lewą stronę równania.

$\text{[math]}$

$\text{[math]}$

Wyznacz deltę i rozwiązania powyższej nierówności.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zauważ, że $\text{[math]}$ nie należy do dziedziny, więc jedynym rozwiązaniem jest $\text{[math]}$

Ćwiczenie sprawdzające 1., strona 39, Matematyka. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 19., strona 124, Matematyka z Plusem. Klasa 1. Podręcznik. Poziom rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 1., strona 244, MATeMAtyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 2., strona 85, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 5, strona 85, NOWA MATeMAtyka 1. Podręcznik. Zakres podstawowy i rozszerzony

Zadanie 9., strona 208, Matematyka. Klasa 3. Zakres rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie 7.7, strona 129, Matematyka. Klasa 2. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zadanie zbadaj to sam 2., strona 61, Matematyka z plusem. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie Prosto do matury – 9.2, strona 30, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 8.22, strona 185, Matematyka i przykłady jej zastosowań. Klasa 1.Podręcznik. Zakres podstawowy i rozszerzony - rozwiązania i odpowiedzi

4

5

6

7

8

10

12

14

16

18

20

22

Zadanie 13

24

24

24

Pełny spis treści