Oblicz długości boków czworokąta wypukłego
wpisanego w okręg o promieniu 4, jeśli kąty
i
są proste, a przekątne
i
przecinają się w punkcie
takim, że
oraz
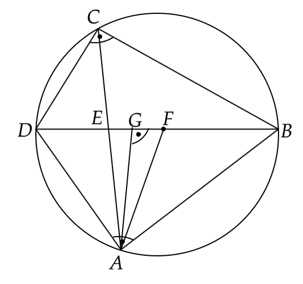
Trójkąt AEF jest równoramienny
.
- kąty wpisane oparte na tym samym łuku
- kąty wierzchołkowe
Trójkąty AEB i DEC są podobne z cechy kąt, kąt, kąt.
ODP: Długości boków czworokąta wynoszą odpowiednio
Wprowadź oznaczenia pomocnicze:
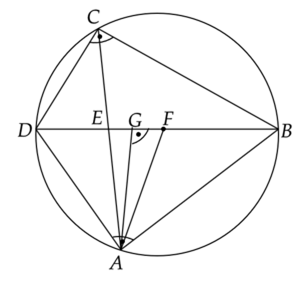
Z treści zadania wiesz, że:
Oznacz jako:
Zauważ, że skoro kąty BCD i ABD są proste to ich przeciwprostokątna jest średnicą okręgu.
Na tej podstawie oblicz długość odcinka AE.
Zauważ, że:
i na podstawie treści zadania oblicz długości odcinków DE i EB.
Zauważ, że trójkąt AEF jest równoramienny, ponieważ
.
Oblicz długość odcinka GF.
Zauważ, że trójkąt AGF jest prostokątny. Skorzystaj z twierdzenia Pitagorasa i oblicz długość odcinka AG.
Zauważ, że trójkąty ABG i ADG są prostokątne. Ponownie skorzystaj z twierdzenia Pitagorasa i oblicz długości odcinków AB i AD.
Zauważ, że
- kąty wpisane oparte na tym samym łuku
- kąty wierzchołkowe
Oznacza to, że trójkąty AEB i DEC są podobne z cechy kąt, kąt, kąt.
Skorzystaj z proporcji i oblicz długość odcinka CD.
Skorzystaj z twierdzenia Pitagorasa w trójkącie BCD i oblicz długość boku BC.
